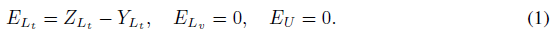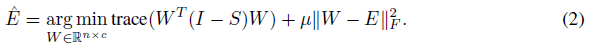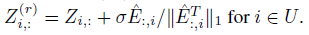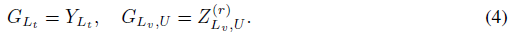Post

【论文笔记】C&S

Posted Updated
By Zhao Zhengyang 15 min read

Combining Label Propagation and Simple Models out-Performs Graph Neural Networks

2021 ICLR

论文链接：https://arxiv.org/pdf/2010.13993

官方代码：https://github.com/CUAI/CorrectAndSmooth

DGL实现：https://github.com/dmlc/dgl/tree/master/examples/pytorch/correct_and_smooth

个人实现：https://github.com/ZZy979/pytorch-tutorial/tree/master/gnn/cs

1.引言

GNN模型越来越复杂，但理解它们的性能提升是一个挑战，另外将它们扩展到大数据集上是困难的

为了提升图学习在直推式顶点分类中的性能，该论文提出了一个简单模型，由三部分组成：

  • 使用顶点特征进行的忽略图结构的基本预测（例如MLP或线性模型）
  • 修正(correct)步骤，从整个图的训练数据中传播不确定性以修正基础预测
  • 对图上的预测进行平滑(smoothing)处理 后两步只是后处理，使用基于图的半监督学习的经典方法，即标签传播(label propagation)

模型框架

在该论文提出的框架中，图结构不用于学习参数，而是用作后处理机制

这种简单性导致模型参数和训练时间少几个数量级，并且可以轻松扩展到大图

该论文性能提升的一个主要来源是直接使用标签进行预测

最近的将GNN与标签传播联系起来的研究训练成本仍然很高，而该论文以两种可理解、低成本的方式使用标签传播

  • 忽略图结构的模型进行“基础预测”
  • 之后使用标签传播进行纠错，然后平滑最终预测 这些后处理步骤基于以下事实：相连顶点上的错误和标签是正相关的，类似于网络分析中相连顶点之间的相似度假设，以及半监督学习中的平滑或聚类假设

该论文的方法表明，结合几个简单的思想，可以在直推式顶点分类中以较小的成本（参数数量和训练时间）产生出色的性能

该论文的主要发现是将标签更直接地纳入学习算法是关键

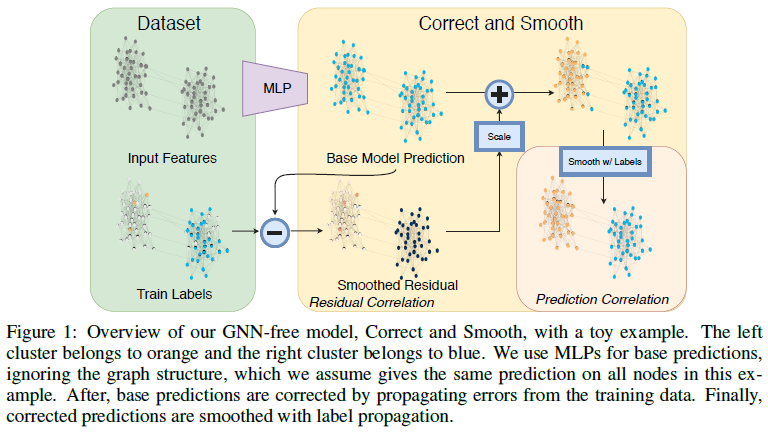
2.C&S模型

假设有一个无向图G=(V, E)，n=|V|是顶点数，顶点特征矩阵 $X \in R^{n \times p}$ ，顶点集合V划分为两个不相交的子集：无标签顶点U和有标签顶点L

顶点标签表示为one-hot矩阵 $Y \in R^{n \times C}$ ，其中C是类别数

该论文的问题是直推式顶点分类：给定G, X和Y，为每个j∈U赋予一个{1, …, C}中的标签

该论文方法首先在顶点特征上使用一个简单的基础预测器，不依赖于图结构；之后进行两种类型的标签传播(LP)：一个通过建模相关误差来修正基础预测，另一个平滑最终预测

这两个方法的组合称为Correct and Smooth (C&S)，见图1

注：

  • 标签传播来自2002年论文 Learning from Labeled and Unlabeled Data with Label Propagation，其核心思想是图中无标签顶点的预测概率等于邻居平均，即 $Y^{(t+1)}=\alpha D^{−\frac{1}{2}}AD^{−\frac{1}{2}}Y^{(t)}+(1−\alpha)Y^{(0)}$ ，其中 $Y^{(t)} \in R^{N \times C}$是预测概率，初始值 $Y^{(0)}$ 对于有标签顶点是one-hot编码，对于无标签顶点是零向量
  • 迭代公式的第一项就是GNN的消息传递（简单的邻居平均），这种方法仅使用标签和图结构信息，无训练参数，无随机性
  • C&S (2)和(4)式对应的迭代公式就来自这篇论文

LP只是后处理步骤，这个流程不是端到端的

另外，图只用在这两个后处理步骤以及一个预处理步骤中（用于增强特征X），并不用于基础预测，这使得与标准GNN模型相比训练更快、更可扩展

2.1 简单基础预测器

简单基础预测器不依赖于图结构

具体地，训练一个模型f来最小化 $\sum_{i \in L_t} \ell(f(x_i), y_i)$，其中 $x_i$ 是顶点i的特征（矩阵X的第i行）， $y_i$ 是顶点i的标签（矩阵Y的第i行），

在该论文中，f是线性模型或浅层MLP加一个softmax，损失函数是交叉熵损失，$L_t$ 是训练集，验证集 $L_v$ 用于调超参数（例如学习率、隐藏层维数）

从模型f可以得到基础预测 $Z \in R^{n \times C}$，基础预测不使用图结构避免了GNN的可扩展性问题

2.2 使用残差传播修正基础预测中的误差

接下来通过将标签结合到相关误差(correlate error)中来提升基础预测Z的准确率

核心思想是我们期望基本预测中的误差沿图中的边呈正相关

换句话说，顶点i的误差增加了顶点i的邻居出现类似误差的机会

我们应该在图上“传播”这种不确定性，该论文的方法部分受到残差传播的启发

为此，首先定义误差矩阵 $E \in R^{n \times C}$，误差对于训练集 $L_t$ 是基础预测和真实标签的差，对于验证集 $L_v$ 和测试集（无标签顶点集合）U是0

公式(1)

  • 阅读代码后注： $E_{L_t}$ 应该是 $Y_{L_t}-Z_{L_t}$

使用标签传播技术来平滑该误差，优化以下目标函数：

公式(2)

其中S是归一化的邻接矩阵 $S=D^{−\frac{1}{2}}AD^{−\frac{1}{2}}$

使用迭代法获得近似最优解： $E^{(t+1)}=(1−\alpha)E+\alpha SE^{(t)},\alpha=\frac{1}{1+\mu},E^{(0)}=E$

注：这个目标函数和迭代公式来自该论文引用的另一篇论文，不需要理解，重点是如何使用最优解 $\hat E$

这个迭代过程是误差的传播和扩散，将平滑后的误差加到基础预测上得到修正的预测 $Z^{(r)}=Z+\hat E$

（(1)式中验证集和测试集没有计算误差，通过这种方式为验证集和测试集也“生成”了误差）

这一步是后处理，与基础预测没有耦合

该论文发现调整 $\hat E$ 的系数会有帮助，因此提出了两种不同的放缩

Autoscale

令 $e_j$ 表示E的第j行，定义 $\sigma=\frac{1}{\vert L_t \vert}\sum_{j \in L_t}{\Vert e_j \Vert}_1$

则无标签顶点i的修正的预测为

Autoscale公式

Scaled Fixed Diffusion (FDiff-scale)

迭代 $E_U^{(t+1)}={[D^{−1}AE^{(t)}]}_U$ ，固定 $E_L^{(t)}=E_L$

即固定有标签顶点的误差，其他顶点不断平均其邻居的值

学习一个超参数s， $Z^{(r)}=Z+s\hat E$

2.3 使用预测相关性平滑最终预测

至此得到了一个得分向量 $Z^{(r)}$ ，为了做最终预测，需要进一步平滑修正的预测

动机是图中相邻的顶点可能具有相似的标签，这符合网络的同质性特征，因此使用另一次标签传播来进行标签分布上的平滑

首先计算“猜测”：

公式(4)

即将训练顶点设置回其真实标签，验证和无标签顶点使用修正的预测

之后迭代 $G^{(t+1)}=(1−\alpha)G+\alpha SG^{(t)},G^{(0)}=G$ ，直到收敛，得到最终预测 $\hat Y$ ，则顶点i∈U的预测标签是 $\arg\max_j {\hat Y}_{ij}$

3.直推式顶点分类实验

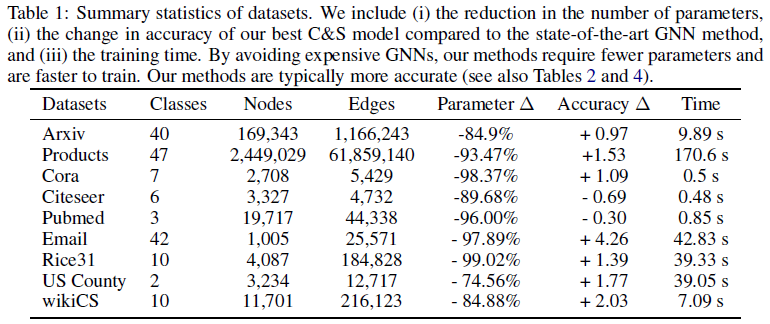
使用9个数据集：

  • OGB: ogbn-arxiv, ogbn-products
  • 论文引用图：Cora, Citeseer, Pubmed
  • 网页图：wikiCS 这些数据集的标签的论文、商品或网页的类别，特征来自文本
  • 社交网络：Rice31，标签是住宅，特征是性别、专业、学年等属性
  • 地理数据集：US Country，标签是2016大选结果，特征是人口统计
  • Email数据集：Email，标签是部门，无特征

数据集

基础预测器和其他模型

使用线性模型和MLP作为基础预测器，输入原始顶点特征和谱嵌入(spectral embedding)

另外还使用了仅使用原始顶点特征的朴素线性模型(Plain Linear)作为对比，以及仅使用标签的标签传播(LP)

为了对比GNN模型和该论文框架，还使用了GCN，添加了残差连接

3.1 顶点分类的初步结果

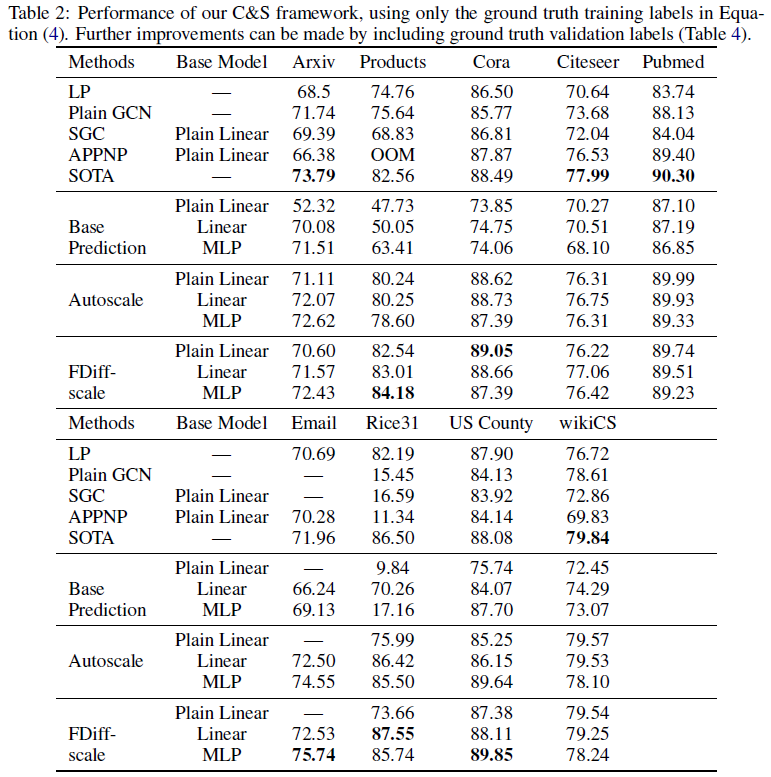
在第一组结果中仅使用训练标签，因为训练GNN模型就是这样做的

顶点分类初步结果

  • 说明（好不容易才看懂）：前5行是Baseline方法，其中LP就是仅使用标签传播；Base Prediction就是仅使用基础预测器；Autoscale和FDiff-scale是该论文的方法，使用两种不同的放缩修正误差方式（见2.2）

结论：

  • 在该论文的模型中，LP后处理步骤有很大的收益（例如，在Products数据集上，MLP基础预测从63%增加到84%）
    • 注：这里说的LP是指Correct和Smooth两个后处理步骤，即仅使用基础预测器和完整C&S模型的对比，不是Baseline中的LP
  • 即使是带有C&S的朴素线性模型（Autoscale和FDiff-scale中的Plain Linear那一行）在许多情况下也足以胜过朴素GCN，而LP（一种没有可学习参数的方法）通常与GCN具有相当的竞争力，这表明将相关性直接纳入图中、简单地使用特征通常是一个更好的主意
  • 该论文的模型变体可以在Products, Cora, Email, Rice31和US Country数据集上表现优于SOTA；在其他数据集上表现最好的模型与SOTA之间没有太大区别

3.2 通过使用更多标签进一步提升

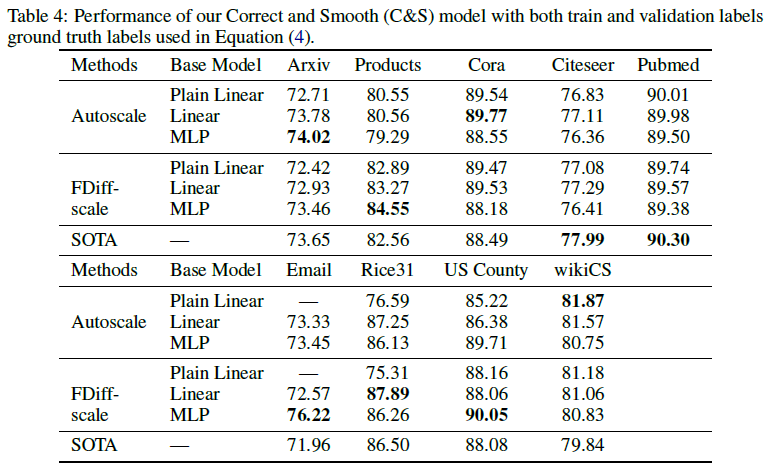
通过在(4)式中使用训练集和验证集标签提升C&S性能

注意不是使用验证集标签来更新基础预测模型，只是用来选择超参数

使用验证集标签提升了更多性能 使用验证集标签的结果

结论：

  • 对于许多数据集上的直推式节点分类，实际上不需要大而昂贵的GNN模型就能获得良好性能
  • 将经典标签传播思想与简单的基础预测器相结合，在这些任务上优于GNN

3.3 更快的训练和改进现有的GNN

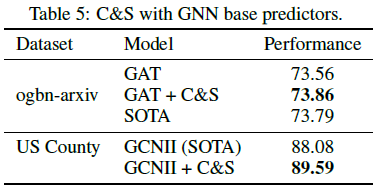
C&S框架需要的参数远少于GNN或其他SOTA方法，因此训练速度比其他模型快几个数量级，而准确率相当

C&S框架也可以用于提升GNN的性能，即将基础预测器替换为更复杂的GCNII或GAT，但性能提升很小，这表明大模型捕获的信号与简单的C&S框架可能是相同的

GNN基础预测器结果

Graph Neural Network
paper note graph neural network
This post is licensed under CC BY 4.0 by the author.