【论文笔记】DCAF
DCAF: A Dynamic Computation Allocation Framework for Online Serving System
论文链接:https://arxiv.org/pdf/2006.09684.pdf
1.引言
现代大型系统(如推荐系统和在线广告系统)基于计算密集型架构,流量增长导致系统压力巨大。此外,请求波动也给在线服务系统带来了严峻挑战(例如双十一购物节)。
应对上述挑战的普遍做法:①将级联系统分解为多个模块,根据经验为每个模块手动分配固定的配额(quota);②涉及算力降级计划,在突发流量高峰时手动执行。
这些策略缺乏灵活性,需要人工干预,并且忽略了请求价值差异。更好的策略是通过偏向价值更高的请求来分配算力。
论文提出了一个动态算力分配框架(Dynamic Computation Allocation Framework, DCAF),目标是在算力预算约束下,对不同价值的流量进行差异化算力分配,从而最大化总收益,同时考虑在线服务系统的稳定性。
3.问题表述
假设一段时间内有N个请求 $i=1,\dots,N$ ,对于每个请求可以采取M种动作 $j=1,\dots,M$ 。 $Q_{ij}$ 定义为请求i分配动作j的预期收益, $q_j$ 为动作j的成本。C表示一段时间内的总算力预算限制。 $x_{ij}$ 表示请求i分配动作j。对于每个请求,有且仅有一个可采取的动作,即 $x_{i\cdot}$ 是one-hot向量。
例如,在广告系统中,j通常表示算力档位; $q_j$ 表示请求在线引擎评估的广告数(配额/最大队列长度),与系统负载正相关; $Q_{ij}$ 表示eCPM (effective cost per mille),与 $q_j$ 正相关(一阶导数为正,但二阶导数为负,即边际收益递减)。
论文将动态算力分配问题表述为背包问题,目标是通过为每个请求i分配适当的动作j,在总算力预算约束下最大化总收益。
\[\mathop{\max}\limits_{j} \sum_{ij} x_{ij}Q_{ij} \quad \text{s.t.} \quad \sum_{ij} x_{ij}q_j \le C, \quad \sum_j x_{ij} \leq 1, \quad x_{ij} \in \{0,1\}\]4.方法论
4.1 全局最优解和证明
首先构造拉格朗日函数
\[\begin{align} L &= -\sum_{ij} x_{ij}Q_{ij} + \lambda (\sum_{ij} x_{ij}q_j - C) + \sum_i (\mu_i (\sum_j x_{ij} - 1)) \\ &= \sum_{ij} x_{ij}(-Q_{ij} + \lambda q_j + \mu_i) - \lambda C - \sum_i \mu_i \\ & \text{s.t.} \quad \lambda \ge 0, \mu_i \ge 0, x_{ij} \ge 0 \end{align}\]这里放松了 $x_{ij}$ 的离散约束。目标是最小化L。
对偶函数为
\[\mathop{\max}\limits_{\lambda,\mu} \mathop{\min}\limits_{x_{ij}} L\]内层最小化,KKT条件:
\[\frac{\partial L}{\partial x_{ij}} = -Q_{ij} + \lambda q_j + \mu_i = 0\]注:
- 物理意义:$\lambda q_j$ 为动作j的加权成本,$\mu_i$ 为请求i的“机会成本”,最优解的边际收益 $Q_{ij}$ 必须等于其边际成本 $\lambda q_j + \mu_i$ 。
- 论文中的解释不太理解:由于 $x_{ij} \ge 0$ ,只有当 $-Q_{ij} + \lambda q_j + \mu_i \ge 0$ 时这个线性函数才是有界的(此时内层最小值显然为0)。而只有当 $-Q_{ij} + \lambda q_j + \mu_i = 0$ 时, $x_{ij} > 0$ 才可能成立($x_{ij}$ 不能全部为0)。
因此对偶问题转化为
\[\begin{align} \mathop{\max}\limits_{\lambda,\mu} (-\lambda C - \sum_i \mu_i) \\ \text{s.t.} \quad -Q_{ij} + \lambda q_j + \mu_i \ge 0, \\ \lambda \ge 0, \mu_i \ge 0, x_{ij} \ge 0 \end{align}\]对偶目标与μ负相关,因此μ的全局最优解为
\[\mu_i^* = \mathop{\max}\limits_{j} (Q_{ij} - \lambda q_j)\]对应的j即为应该分配给请求i的最优动作(与λ有关),即 $x_{ij^*} = 1$
\[j^* = \mathop{\arg \max}\limits_{j} (Q_{ij} - \lambda q_j)\]注:
- 也就是说,对于每次请求,应该选择使(收益-λ*成本)最大的动作。
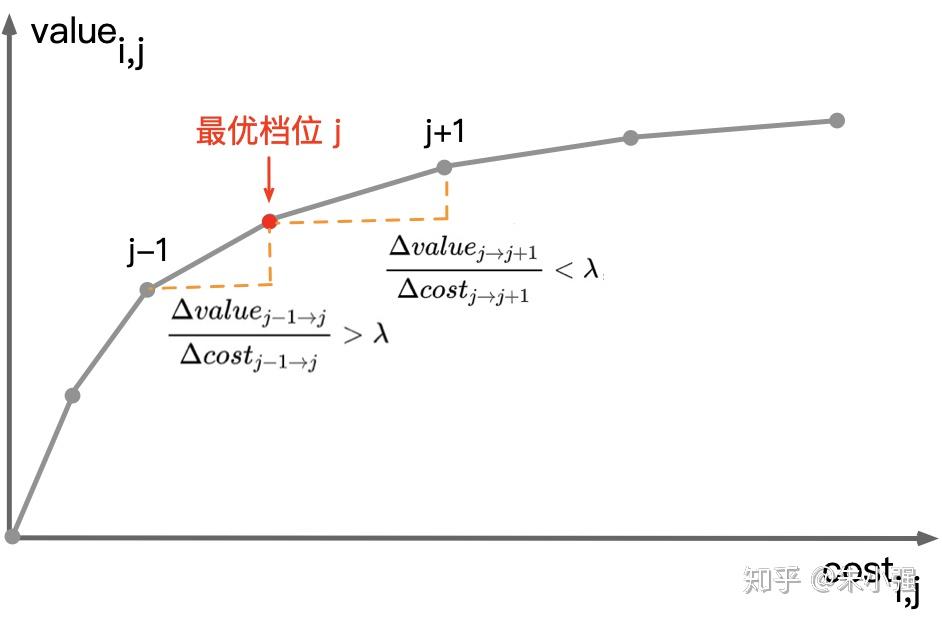
- λ的含义:算力边际收益的约束(即“性价比”增量的临界值)。对于请求i,给定λ,若动作j1优于动作j2,则 $Q_{ij_1} - \lambda q_{j_1} > Q_{ij_2} - \lambda q_{j_2}$ ,即 $\frac{\Delta Q}{\Delta q} > \lambda$ ,如下图所示。
4.2 参数估计
4.2.1 拉格朗日乘子
假设4.1 $Q_{ij}$ 随着j单调递增。
假设4.2 $\frac{Q_{ij}}{q_j}$ 随着j单调递减(边际效用递减规律)。
引理1 如果假设4.1和4.2成立,那么 $\frac{Q_{ij^*}}{q_{j^*}}$ 随着λ单调递增。
注:
- 由 $\mu_i^* = Q_{ij^*} - \lambda q_{j^*} \ge 0$ 可得 $\frac{Q_{ij^*}}{q_{j^*}} \ge \lambda$
- 由假设4.2和引理1可得 j* 随着λ单调递减。
引理2 如果假设4.1和4.2成立,那么 $\sum_{ij} x_{ij}Q_{ij} = \sum_i Q_{ij^*}$ (总收益)和 $\sum_{ij} x_{ij}q_j = \sum_i q_{j^*}$ (总成本)都随着λ单调递减。
定理1 如果引理2成立,则全局最优的拉格朗日乘子 λ* 可通过二分搜索找到,使得 $\sum_{ij} x_{ij}q_j = C$ 成立。
注:即满足以下两个条件时达到全局最优解
- $\frac{\partial Q_{ij}}{\partial q_j} = \lambda^*$ (即所有请求的边际收益都是λ*)
- $\sum_{ij} x_{ij}q_j = C$ (即恰好把算力预算用完)
搜索最优拉格朗日乘子的算法如下:
对于更一般的情况,可以使用更复杂的方法,例如强化学习。
4.2.2 请求预期收益
在电商领域,预期收益通常定义为线上性能指标(如eCPM)。主要使用四类特征:用户画像、用户行为、上下文和系统状态。
5.架构
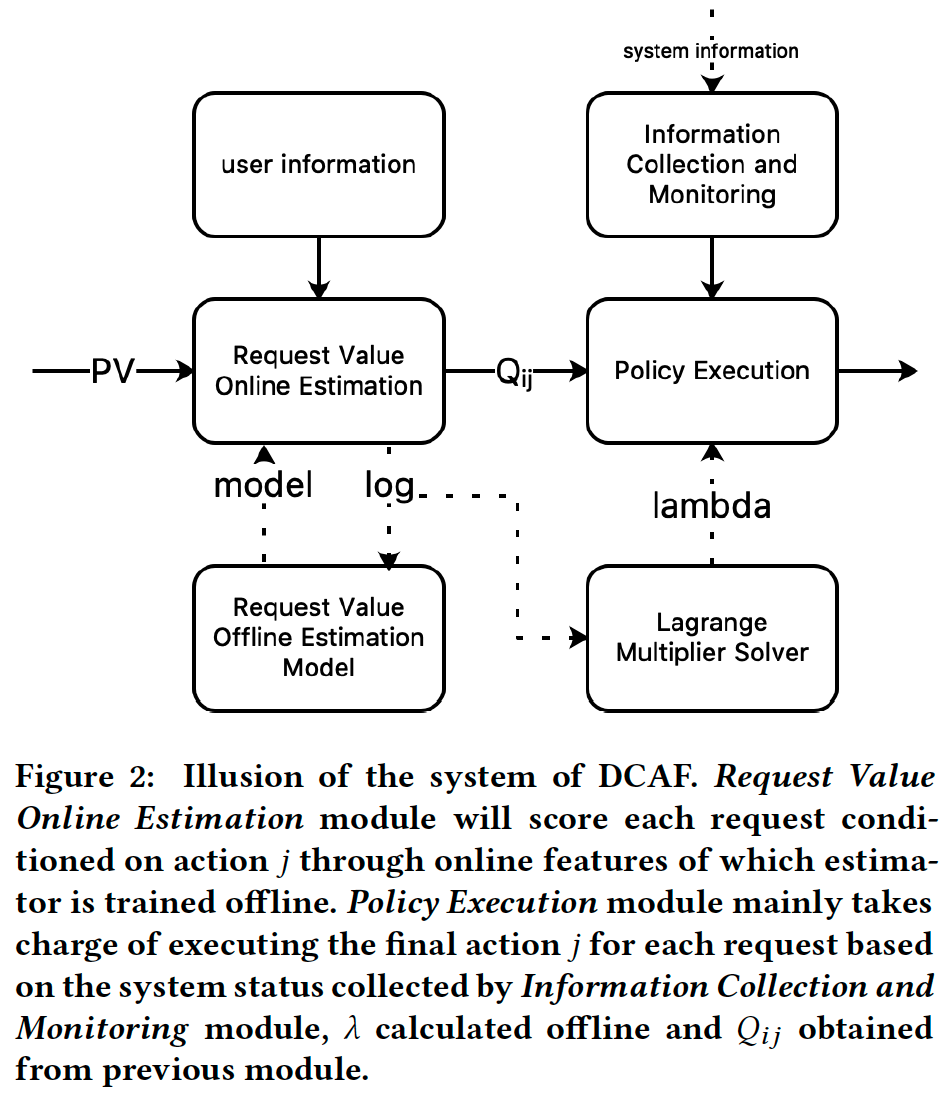
DCAF由在线决策器和离线估计器组成,结构如下图所示。
5.1 在线决策器
5.1.1 信息收集和监控
该模块监控并提供系统当前状态信息,包括GPU利用率、CPU利用率、耗时、失败率等。
5.1.2 请求价值估计
该模块基于信息收集模块提供的特征估计请求的价值 $Q_{ij}$ 。
5.1.3 策略执行
该模块根据公式(6)(4.1节结尾)为请求i分配最佳动作 j* 。为了保证在线系统的稳定性,论文提出了一个称为MaxPower的概念,它是每次请求必须遵循的 $q_j$ 的上界。MaxPower的引入保证了系统在遇到突发请求高峰时能够及时、自动地自我调整并保持稳定。
注:为什么需要MaxPower,而不能依靠DCAF自动调节?当遇到突发请求高峰时,系统的耗时和失败率大幅上升,此时DCAF调节所依赖的数据(如系统总算力C)已经不可信了。
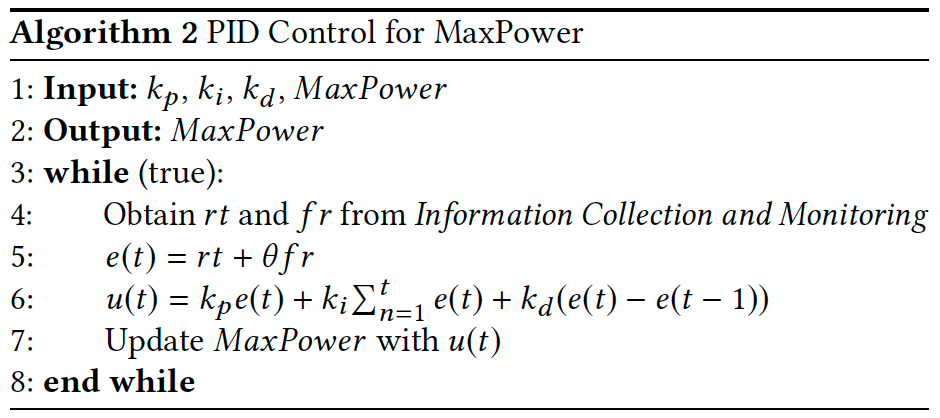
MaxPower由PID机制自动控制:
\[u(t) = k_p e(t) + k_i \sum_{n=1}^t e(n) + k_d (e(t) - e(t-1))\]u(t)和e(t)分别是t时刻的控制动作和系统不稳定性。对于e(t),将其定义为一段时间内平均耗时(rt)和失败率(fr)的加权和,即 $e(t) = rt + \theta fr$ 。
5.2 离线估计器
5.2.1 拉格朗日乘子求解器
如上所述,可以通过简单的二分搜索得到拉格朗日乘子的全局最优解。在实际中,使用日志数据作为输入:
- 从日志中采样N条记录,得到 $Q_{ij}$ 、 $q_j$ 和算力成本C(例如在一段时间内请求CTR模型的广告总数)。
- 根据当前系统状态调整算力成本:C * 常规QPS / 当前QPS,这可以使N条记录在当前算力约束之下。
- 使用算法1搜索最优的拉格朗日乘子。
注:也可以用PID来调节λ。根据引理2,使用的总算力随着λ单调递减。如果一段时间内实际使用的总算力小于C,则调小λ;否则调大λ。
5.2.2 预期收益估计器
在广告系统中,对于每次请求,$Q_{ij}$ 为不同动作j下的eCPM。由于eCPM = CTR * bid,其中bid为广告主出价,因此使用CTR模型来估计点击率(CTR)。CTR模型受动作的影响(例如算力档位决定广告队列长度),因此必须估计不同动作下的请求收益。这个估计器会定期更新,并在策略执行模块提供实时推理。
6.实验
6.1 离线实验
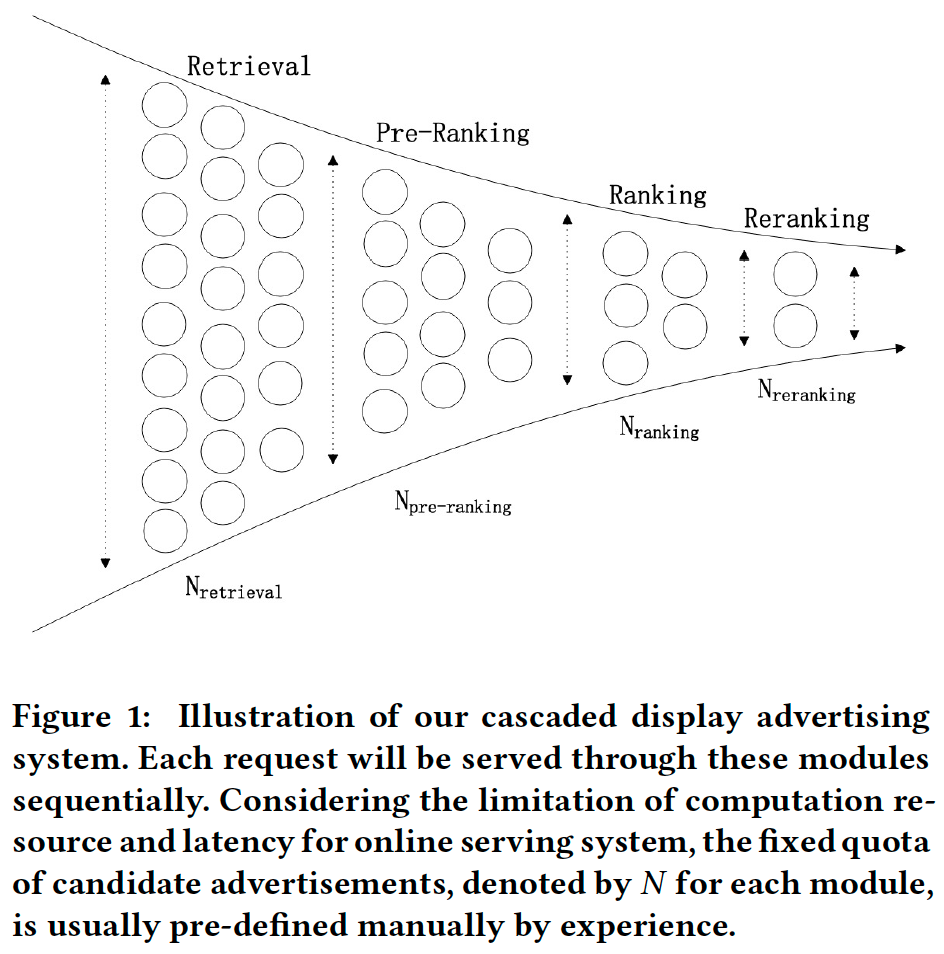
从淘宝广告系统收集了真实日志,并进行离线实验。通过离线日志模拟了DCAF在Ranking阶段(如图1所示)的性能:
- 动作j控制Ranking阶段需要由CTR模型预估的广告数
- $q_j$ 表示请求CTR模型的广告配额
- $Q_{ij}$ 是在Ranking阶段请求i选择动作j的条件下top-k广告的eCPM总和
- C表示一段时间内请求CTR模型的广告总数
- Baseline:为不同请求分配相同的算力(Ranking阶段广告数)
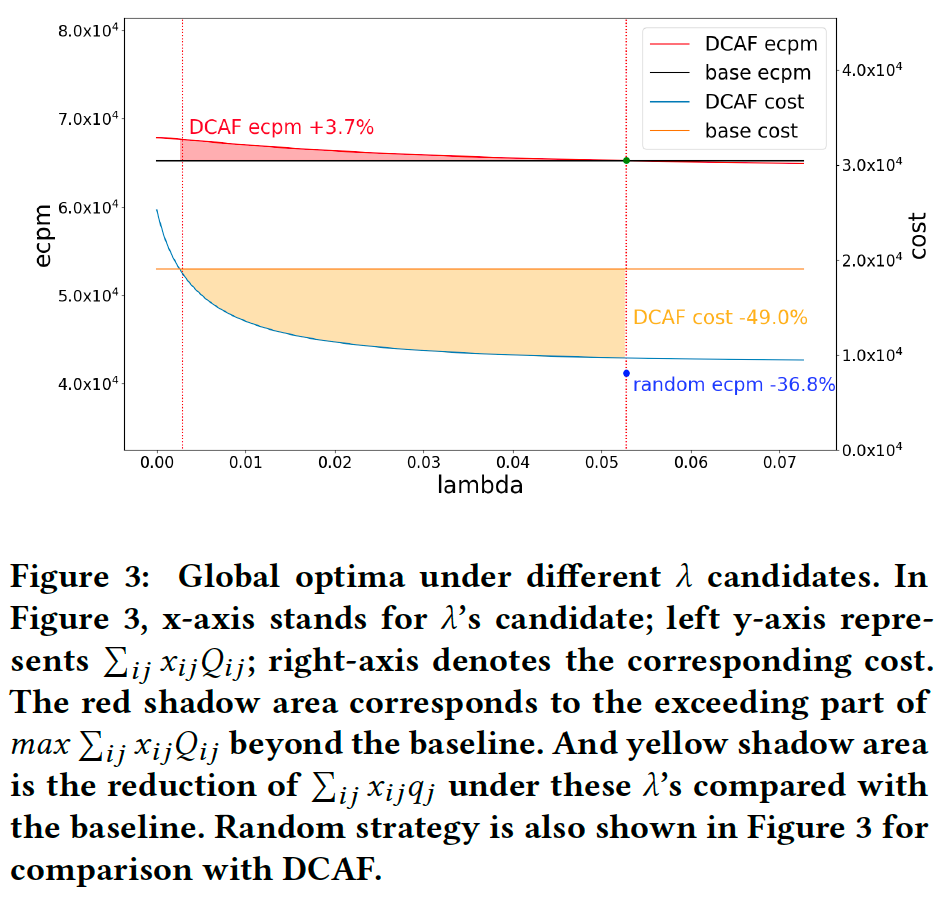
图3展示了λ与实际收益和对应算力成本之间的关系。红色区域对应DCAF的收益超过baseline的部分,黄色区域对应DCAF的成本比baseline减少的部分。这说明当λ位于适当的区间(两条虚线)时,DCAF的表现优于baseline:可以用相同的算力达到更高的收益,或者用更少的算力达到相同的收益。
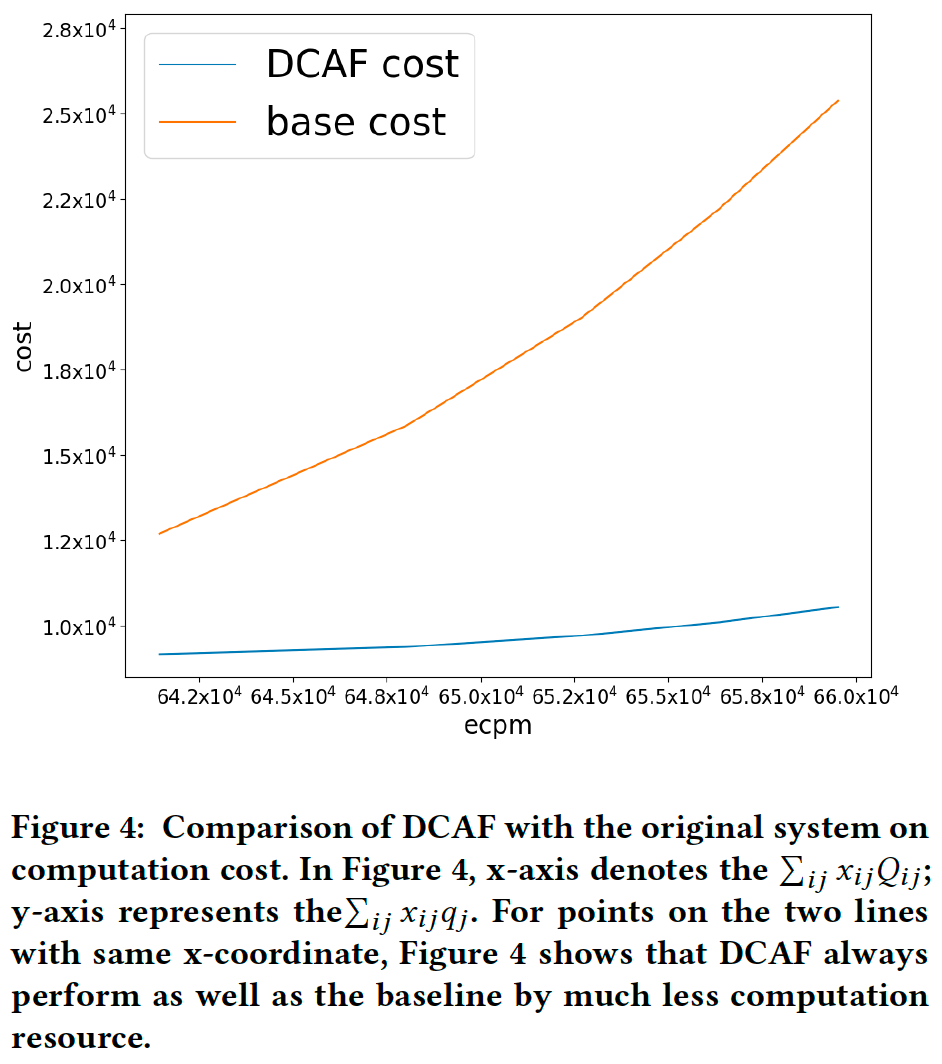
图4展示了DCAF与原始系统的算力成本比较。DCAF始终能够达到与baseline相同的性能,并大幅节省成本。
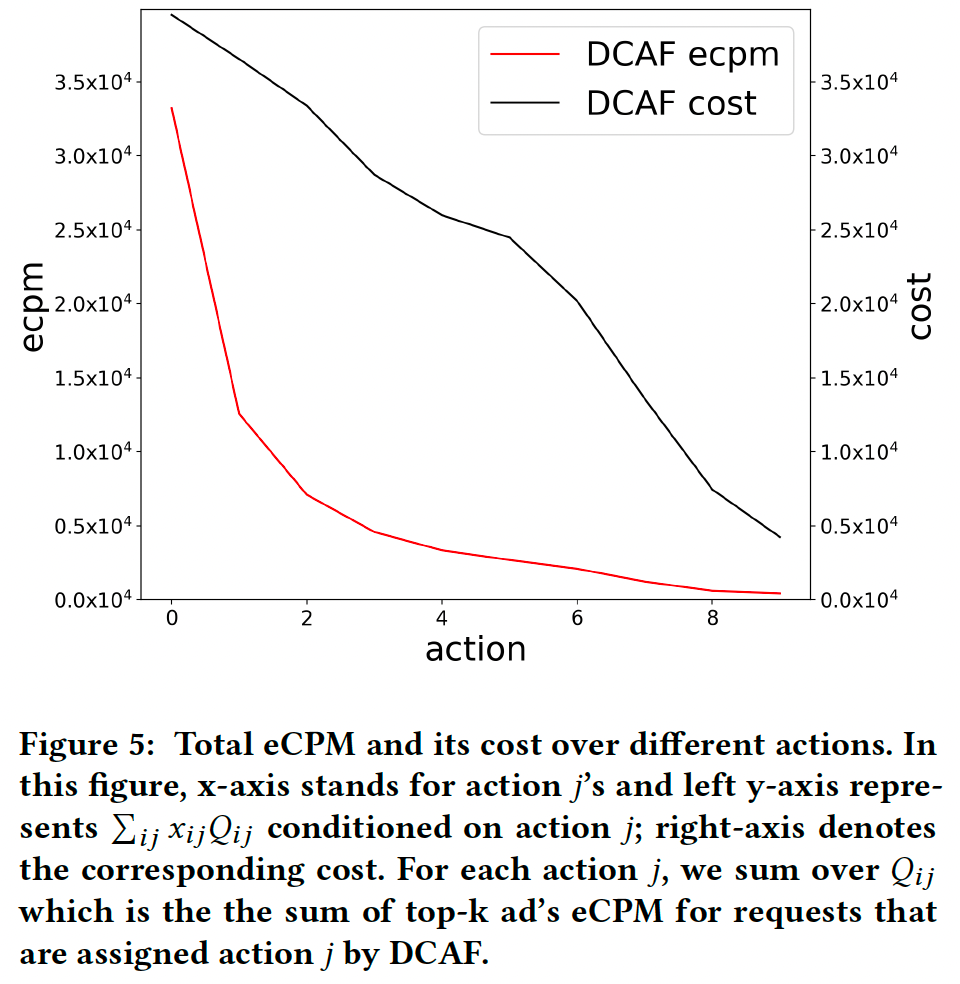
图5展示了不同动作的收益和成本。可以看出DCAF通过采取不同的动作区别对待每次请求。且收益/成本随着动作递减,这表明遵循边际效用递减规律。
(疑问:根据前文描述,收益和成本随着动作j递增,另外边际效用递减说明红线应该是上凸而不是下凸,因此这张图应该上下翻转?)
6.2 在线实验
2020.5.20至2020.5.30在阿里巴巴广告系统进行了线上A/B实验以验证DCAF的有效性。在线实验的设置与离线实验基本相同。DCAF部署在Pre-Ranking阶段和Ranking阶段之间,旨在动态分配Ranking的CTR模型消耗的GPU资源。
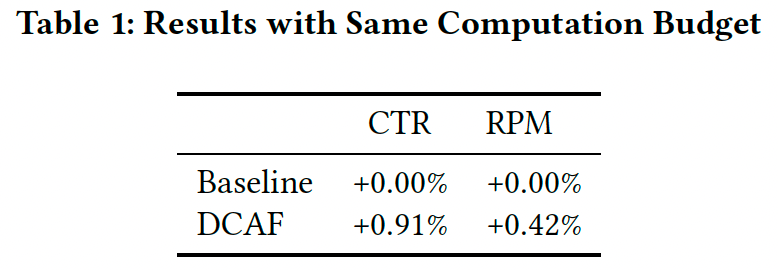
表1显示,DCAF可以带来收益提升而使用相同的算力成本。
RPM: Revenue Per Mille 千次展示收入
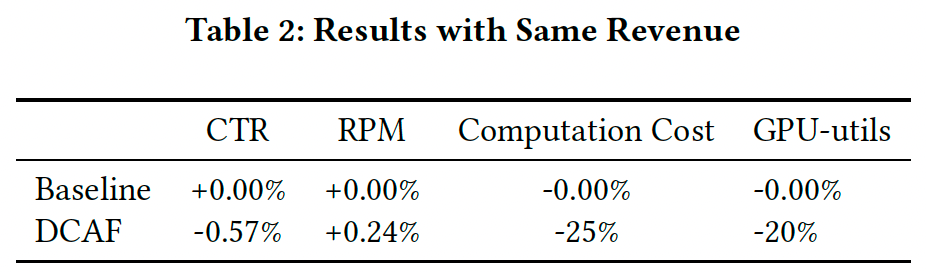
表2显示,DCAF在保持相同收益的情况下将算力成本(请求CTR模型的广告总数)降低了25%,GPU资源利用率降低了20%。
在线上系统中,$Q_{ij}$ 是通过一个简单的线性模型估计的,可能不足以完全捕获数据分布。因此DCAF在线上系统中的提升小于离线实验结果。
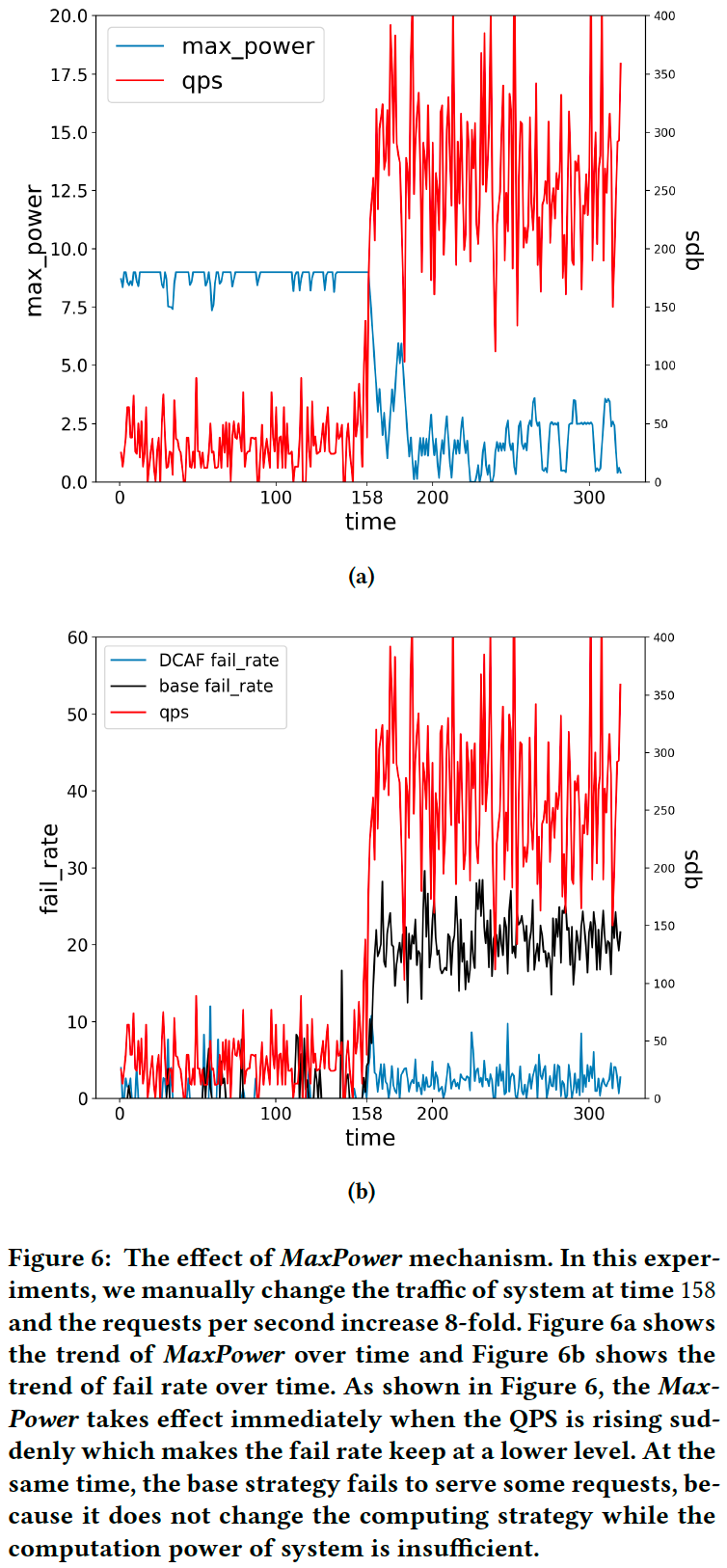
图6展示了在双十一等极端情况的流量压力下DCAF的性能。通过MaxPower的控制机制,在线服务系统可以快速应对流量突增,并通过将失败率和耗时保持在较低水平从而使系统恢复正常状态。在这种情况下,MaxPower的控制机制优于人为干预。