【DGL教程】第2章 消息传递

官方文档：https://docs.dgl.ai/guide/message.html

1.消息传递模型

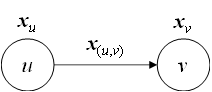
令 $x_v \in R^{d_1}$ 表示顶点v的特征，$x_{(u,v)} \in R^{d_2}$表示边(u, v)的特征，$m_{(u,v)}$表示边(u, v)的消息，消息传递模型定义如下：

\[m_{(u,v)}^{(t+1)} = \phi (x_u^{(t)},x_v^{(t)},x_{(u,v)}^{(t)}) \cdots (1)\] \[x_v^{(t+1)} = \psi (x_v^{(t)},\rho (\{m_{(u,v)}^{(t+1)}|u \in N(v)\})) \cdots (2)\]

其中，φ是定义在边上的消息函数，通过组合边及其关联的顶点的特征来产生消息；ψ是定义在顶点上的更新函数，通过使用归约函数ρ聚集顶点收到的消息（即该顶点所有关联的边所产生的消息）来更新顶点的特征

即消息函数描述以下过程：

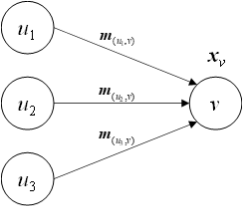
\[\left. \begin{matrix} x_u \newline x_v \newline x_{(u,v)} \end{matrix} \right\rbrace \stackrel{?}{\longrightarrow} m_{(u,v)}\]

归约函数描述以下过程：

\[\left. \begin{matrix} m_{(u_1,v)} \newline m_{(u_2,v)} \newline m_{(u_3,v)} \end{matrix} \right\rbrace \stackrel{?}{\longrightarrow} x_v\]

2.内置函数和消息传递API

dgl.function包提供了常用的消息函数和归约函数

2.1 消息函数

DGL的内置消息函数遵循统一的命名格式：<操作数1>_<运算符>_<操作数2>，其中“操作数”可以是u, v, e，分别表示起点、终点、边；“运算符”可以是add, sub, mul, div, dot

内置消息函数有三个参数f1, f2, out，均为字符串，表示“操作数1”的特征f1和“操作数2”的特征f2进行某种计算，输出的消息作为边的特征out

例如：u_add_v('hu', 'hv', 'm')表示通过将一条边的起点特征hu和终点特征hv相加来生成消息，作为该边的特征m

DGL还支持两个一元内置消息函数copy_u(f, out)和copy_e(f, out)，分别表示直接将起点/边的特征f作为消息，作为边的特征out

注意：虽然消息传递模型中的消息函数φ有起点特征、终点特征和边特征三个参数，但DGL中的内置消息函数是一元或二元的，即操作数只能三选一或三选二

完整列表：https://docs.dgl.ai/api/python/dgl.function.html#message-functions

自定义消息函数

官方文档：https://docs.dgl.ai/api/python/udf.html#apiudf

当内置消息函数不能满足要求时，可以自定义消息函数，格式如下：

def message_func(edges):
    return {'m': f(edges.src['hu'], edges.dst['hv'], edges.data['he'])}

其中edges是EdgeBatch类型的对象（可以理解为一批要生成消息的边），edges.src, edges.dst, edges.data分别表示起点、终点和边本身的特征

内置消息函数u_add_v('hu', 'hv', 'm')即等价于

def message_func(edges):
    return {'m': edges.src['hu'] + edges.dst['hv']}

2.2 归约函数

DGL提供的内置归约函数有sum, max, min, mean，即分别对顶点收到的消息进行求和、取最大值、取最小值、取平均

内置归约函数有两个参数msg和out，均为字符串，分别表示消息所在的边特征名称和输出的顶点特征名称

例如：sum('m', 'h')表示将一个顶点的所有入边的特征m求和，作为该顶点的特征h

完整列表：https://docs.dgl.ai/api/python/dgl.function.html#reduce-functions

自定义归约函数

自定义归约函数的格式如下：

def reduce_func(nodes):
    return {'h': f(nodes.mailbox['m'])}

其中nodes是NodeBatch类型的对象（可以理解为一批要聚集消息的顶点），nodes.mailbox和nodes.data分别表示收到的消息和顶点本身的特征

内置归约函数sum('m', 'h')等价于

def reduce_func(nodes):
    return {'h': torch.sum(nodes.mailbox['m'], dim=1)}

2.3 消息传递API

消息计算API：dgl.DGLGraph.apply_edges(message_func)，对应消息传递模型的公式(1)

• 参数是消息函数
• 例如：g.apply_edges(dgl.function.u_add_v('hu', 'hv', 'he'))

顶点更新API：dgl.DGLGraph.update_all(message_func, reduce_func)，对应消息传递模型的公式(1)+(2)

• 两个参数分别为消息函数和归约函数（更新函数默认使用计算出的特征覆盖原来的特征）
• 该方法是一个高层次API，在一次调用中执行了消息生成（使用消息函数）、消息归约（使用归约函数）和顶点更新
• 该API在dgl.nn.pytorch.conv包的卷积模块中被广泛使用

例如，下面的代码通过将起点特征ft与边特征a按元素相乘来生成消息m，通过对消息m求和来更新顶点特征ft，最后将ft乘2得到最终结果final_ft

import dgl.function as fn

def update_all_example(graph):
    # store the result in graph.ndata['ft']
    graph.update_all(fn.u_mul_e('ft', 'a', 'm'), fn.sum('m', 'ft'))
    # Call update function outside of update_all
    final_ft = graph.ndata['ft'] * 2
    return final_ft

对应的数学公式为

\[final\_ft_v = 2\sum_{u \in N(v)}{ft_u * a_{(u,v)}}\]

实例

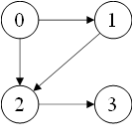
假设图结构如下

>>> g = dgl.graph((torch.tensor([0, 0, 1, 2]), torch.tensor([1, 2, 2, 3])))

顶点有一个特征x（数值类型必须是浮点数，否则会报错）：

>>> g.ndata['x'] = torch.tensor([[0, 1], [1, 2], [2, 3], [3, 4]], dtype=torch.float)

消息函数为起点和终点的特征x的积，归约函数为消息的和，即：

\[m_{(u,v)}^{(t+1)} = x_u^{(t)} * x_v^{(t)}\] \[x_v^{(t+1)} = \sum_{u \in N(v)}m_{(u,v)}^{(t+1)}\]

则一次消息传递的过程如下：

>>> g.update_all(fn.u_mul_v('x', 'x', 'm'), fn.sum('m', 'x'))
>>> g.ndata['x']
tensor([[ 0.,  0.],
        [ 0.,  2.],
        [ 2.,  9.],
        [ 6., 12.]])

v	$x_v^{(0)}$		e	$m_e^{(1)}$		v	$x_v^{(1)}$
0	[0, 1]		(0, 1)	[0, 2]		0	[0, 0]
1	[1, 2]	→	(0, 2)	[0, 3]	→	1	[0, 2]
2	[2, 3]		(1, 2)	[2, 6]		2	[2, 9]
3	[3, 4]		(2, 3)	[6, 12]		3	[6, 12]

解释：

$m_{(0,1)}^{(1)}=x_0^{(0)} * x_1^{(0)}=[0 \times 1,1 \times 2]=[0,2]$，其他同理

$x_2^{(1)}=m_{(0,2)}^{(1)}+m_{(1,2)}^{(1)}=[0,3]+[2,6]=[2,9]$，其他同理

2.4 异构图的消息传递API

dgl.DGLHeteroGraph.multi_update_all(etype_dict, cross_reducer)

• 参数etype_dict是一个字典，键是一个关系（字符串三元组或一个字符串，表示边类型），值是一个元组(message_func, reduce_func)，含义和update_all()相同
• 参数cross_reducer是一个字符串，表示如何对来自不同类型的边的消息进行归约，可选项为'sum', 'min', 'max', 'mean', 'stack'

实例

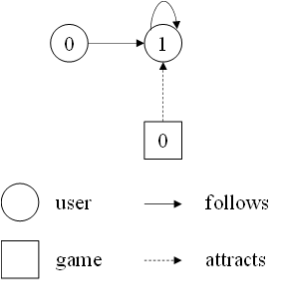
创建一个包含“用户”和“游戏”两种顶点、“关注”和“吸引”两种边的异构图：

>>> g = dgl.heterograph({
    ('user', 'follows', 'user'): ([0, 1], [1, 1]),
    ('game', 'attracts', 'user'): ([0], [1])
})
>>> g.nodes['user'].data['h'] = torch.tensor([1., 2.])
>>> g.nodes['game'].data['h'] = torch.tensor([3.])
>>> g.ndata
{'game': {'h': tensor([3.])}, 'user': {'h': tensor([1., 2.])}}

消息传递过程如下：

>>> g.multi_update_all({
    'follows': (fn.copy_u('h', 'm'), fn.max('m', 'h')),
    'attracts': (fn.u_add_v('h', 'h', 'm'), fn.sum('m', 'h'))
}, 'stack')
>>> g.nodes['user'].data['h']
tensor([[0., 0.],
        [5., 2.]])
>>> g.nodes['game'].data['h']
tensor([3.])

user	$h_{user}^{(0)}$		follows	$m_{follows}^{(1)}$		user	$h_{user}^{(1)}$
0	1	→	(0, 1)	1	↘	0	[0, 0]
1	2	→	(1, 1)	2	→	1	[5, 2]
game	$h_{game}^{(0)}$	↘	attracts	$m_{attracts}^{(1)}$	↗	game	$h_{game}^{(1)}$
0	3	→	(0, 1)	5		0	3（未更新）

解释：

$m_{follows(0,1)}^{(1)}=x_{user0}^{(0)}=1,m_{attracts(0,1)}^{(1)}=x_{game0}^{(0)}+x_{user1}^{(0)}=2+3=5$

$x_{user1}^{(1)}=sum\lbrace m_{attracts(0,1)}^{(1)}\rbrace \oplus \max\lbrace m_{follows(0,1)}^{(1)},m_{follows(1,1)}^{(1)} \rbrace=sum\lbrace 5\rbrace\oplus \max\lbrace 1,2\rbrace=[5, 2]$