【论文笔记】GAT
Graph Attention Networks
2018 ICLR
代码:
- 官方代码:https://github.com/PetarV-/GAT
- DGL实现:https://github.com/dmlc/dgl/tree/master/examples/pytorch/gat
- 个人实现: https://github.com/ZZy979/pytorch-tutorial/tree/master/gnn/gat
1.引言
CNN已经被成功地用于解决图像分类、语义分段、机器翻译等问题,这些问题的数据表示都是网格结构,而在3D网格、社交网络、交通网络、生物网络、脑连接组等问题中,数据是图结构的。
将卷积操作推广到图领域通常有频域方法和非频域方法。
频域方法通过计算图的拉普拉斯矩阵的特征分解在傅立叶域中定义卷积运算;非频域方法直接在图上定义卷积,对空间上紧密相邻的组进行运算。
注意力机制在很多基于序列的任务中已经成为标准。注意机制的好处之一是允许处理可变大小的输入,关注输入中最相关的部分以做出决策。当注意力机制用于计算单个序列的表示时,通常称为自注意力。
该论文提出一种基于注意力机制的模型来在图结构数据上进行顶点分类。
2.GAT模型
2.1 图注意力层
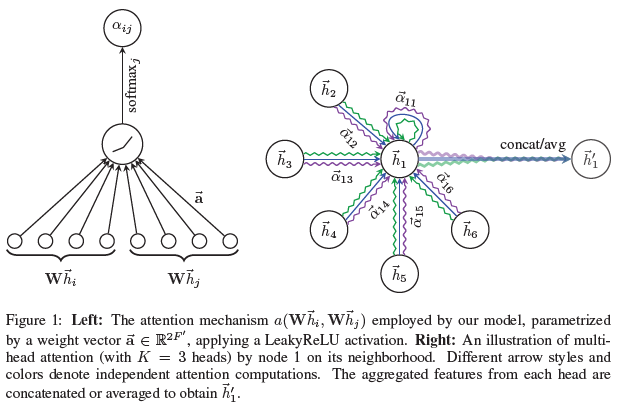
图注意力层是GAT模型的构建块,结构如下图所示
输入是一组顶点特征$H=\lbrace h_1,h_2,…,h_N\rbrace,h_i \in R^F$,N是顶点数,F是顶点特征维数
输出是一组新的顶点特征$H’=\lbrace h_1’,h_2’,…,h_N’\rbrace,h_i’ \in R^{F’}$
对每个顶点应用自注意力机制$a:R^{F’} \times R^{F’} \to R$来计算注意力参数
\[e_{ij}=a(Wh_i,Wh_j ),j \in N_i\]其中$W \in R^{F’ \times F}$是权重矩阵,$N_i$表示顶点i的邻居,$e_{ij}$表示顶点j对顶点i的重要性(下面会说明a具体是什么)
对$e_{ij}$进行归一化
\[\alpha_{ij}=softmax(e_{ij})=\frac{\exp(e_{ij})}{\sum_{k \in N_i}\exp(e_{ik})}\]在该论文中,a是一个单层的前馈神经网络(将两个输入向量进行拼接并计算内积),参数是权重向量$a \in R^{2F’}$,激活函数为LeakyReLU(负斜率为0.2),即
\[e_{ij}=LeakyReLU(a^T (Wh_i || Wh_j))\]其中||表示向量拼接
这一步对应图1(a)
计算出$\alpha_{ij}$后,将其作为权重计算每个顶点的邻居特征的线性组合,得到输出特征
\[h_i'=\sigma \left(\sum_{j \in N_i}{\alpha_{ij}Wh_j} \right)\]为了增强自注意力学习过程的稳定性,论文中将其扩展到多头注意力,即以上过程执行K次,并将结果向量拼接在一起
\[h_i'={||}_{k=1}^K \sigma \left(\sum_{j \in N_i}{\alpha_{ij}^kW^kh_j} \right)\]对于最后一层(预测层),多头注意力采用平均而不是拼接
\[h_i'=\sigma \left(\frac{1}{K}\sum_{k=1}^K{\sum_{j \in N_i}{\alpha_{ij}^kW^kh_j}} \right)\]这一步对应图1(b)
2.2 和相关工作的对比
上一节提出的图注意力层解决了之前方法中的几个问题:
- 计算高效,可并行化
- 与GCN相比,允许给同一个顶点的不同邻居赋予不同的重要性
- 注意力机制对所有的边计算方式相同,因此不依赖于图结构
- 图不需要是无向图
- 模型可用于归纳式学习,即测试图在训练时完全没见过
3.实验
3.1 数据集
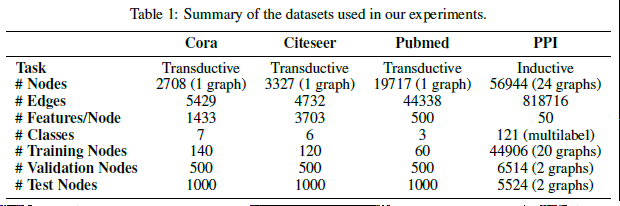
- 直推式(transductive):3个标准引用网络数据集Cora, Citeseer和Pubmed,都只有1个图,其中顶点表示文档,边表示引用(无向),顶点特征为文档的词袋表示,每个顶点有一个类标签
- 归纳式(inductive):蛋白质-蛋白质反应数据集(PPI),由24个图组成,对应人体组织,每个顶点有多个类标签(共121个类别)
3.2 SOTA方法
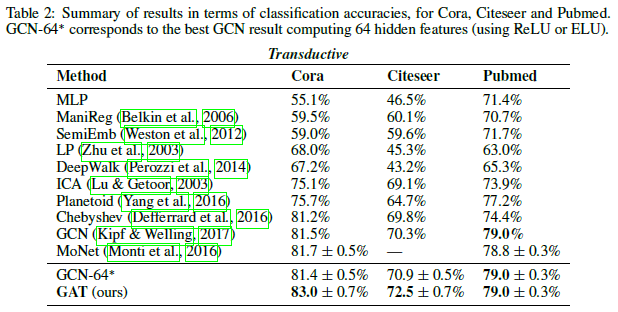
- 直推式:MLP, LP, SemiEmb, ManiReg, DeepWalk, ICA, Planetoid, GCN, Chebyshev, MoNet
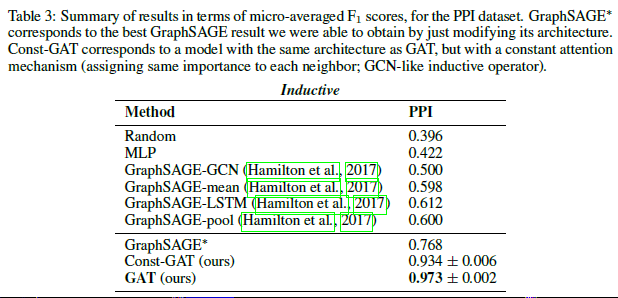
- 归纳式:MLP, GraphSAGE的几种变体(用不同的方式聚集采样邻居的特征),Const-GAT(GAT的变体,所有邻居赋予相同的权重)
3.3 实验设置
- 直推式:两层GAT模型,第一层K=8, F’=8(相当于输出特征维数为64),激活函数为ELU;第2层用于分类,K=1, F’=C, C为类别数,激活函数为softmax
- 归纳式:三层GAT模型,前两层K=4, F’=256(相当于输出特征维数为1024),激活函数为ELU;最后一层用于(多标签)分类,K=6, F’=121(对应类别数),输出结果求平均,加上sigmoid激活函数,训练过程中batch size为2