【论文笔记】GCN

Semi-Supervised Classification with Graph Convolutional Networks

2017 ICLR

论文链接：https://arxiv.org/pdf/1609.02907

代码：

• 官方代码：
  • https://github.com/tkipf/gcn
  • https://tkipf.github.io/graph-convolutional-networks/
• DGL实现：https://github.com/dmlc/dgl/tree/master/examples/pytorch/gcn
• 个人实现： https://github.com/ZZy979/pytorch-tutorial/tree/master/gnn/gcn

开幕雷击！这篇论文一上来就是各种公式推导！如果没有足够的数学知识看这篇论文比较困难。。

这里只用最简单的方式讲一个问题：什么是图卷积

一些基本概念：每个图都有邻接矩阵A，度矩阵D是一个对角矩阵，$D_{ii}=\sum_j A_{ij}$表示顶点i的度，（定义）规范化的对称邻接矩阵$\widetilde A=D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$（对角矩阵的-1/2次方就是每个元素变为-1/2次方）

所谓图卷积，就是$H=\rho (\widetilde AXW)$，其中$X \in R^{n \times m}$ 是输入的特征矩阵，$W \in R^{m \times k}$是一个线性变换，ρ是激活函数，$H \in R^{n \times k}$是输出的顶点特征

将多个图卷积层连接起来就是$H^{(i+1)}=\rho (\widetilde AH^{(i)}W),H^{(0)}=X$

仅此而已

参考DGL的图卷积实现dgl.nn.pytorch.conv.graphconv.GraphConv.forward()，就是一次特征转换（矩阵相乘）+一次消息传递

消息传递的方式也很简单，消息函数就是直接复制起点的特征，归约函数就是求和，因此整个消息传递规则就是使用邻居特征的和来更新顶点特征

因此公式中的乘以邻接矩阵⇔消息传递⇔使用邻居特征求和来更新顶点特征

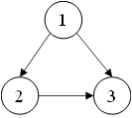
考虑一个简单的图

从矩阵相乘的角度：邻接矩阵$A=\left( \begin{matrix} 0&0&0 \newline 1&0&0 \newline 1&1&0 \end{matrix} \right)$，特征矩阵$X=\left( \begin{matrix} x_1\newline x_2 \newline x_3 \end{matrix} \right)$，则$AX=\left( \begin{matrix} 0 \newline x_1 \newline x_1+x_2 \end{matrix} \right)$

从消息传递的角度：每个顶点的特征变为其邻居特征的和

可以非常直观地理解