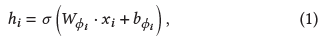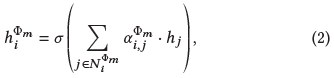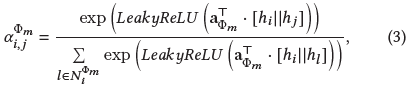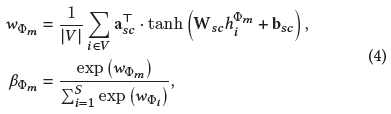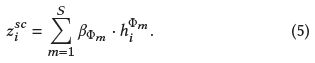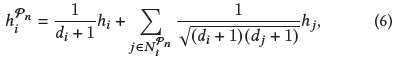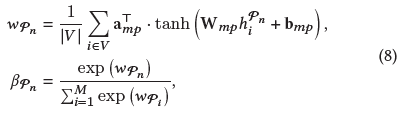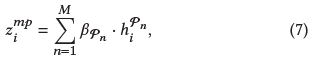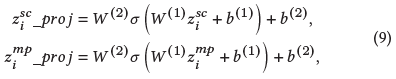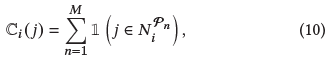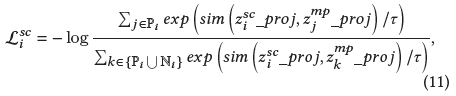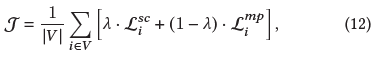Post

【论文笔记】HeCo

Posted Updated
By Zhao Zhengyang 15 min read

Self-Supervised Heterogeneous Graph Neural Network with Co-Contrastive Learning

2021 KDD

论文链接：https://arxiv.org/pdf/2105.09111

官方代码：https://github.com/liun-online/HeCo （少见的作者代码写得清楚又简单）

个人实现：https://github.com/ZZy979/pytorch-tutorial/tree/master/gnn/heco

1.引言

大部分HGNN研究属于半监督学习，即设计不同的异构图消息传递机制来学习顶点嵌入，学习过程由一部分顶点标签监督，然而在某些真实世界环境下获取标签是具有挑战性的且昂贵的

自监督学习旨在从数据本身自发地发现监督信号，成为没有显式标签设定的一个有希望的解决方案

对比学习(contrastive learning) 是一种典型的自监督学习技术，吸引了大量注意力

对比学习旨在通过提取数据中的正负样本，最大化正样本之间的相似度，同时最小化负样本之间的相似度，通过这种方式，即使没有标签也能够学习到有区分度的嵌入

对比学习在CV和NLP领域已被广泛使用，但很少有研究用于异构信息网络(HIN)

在实践中，设计使用对比学习的HGNN并非易事，需要解决以下三个基本问题：

  • 如何设计异构对比机制：HIN具有复杂的结构，元路径能够反映HIN的一个方面，但仅在元路径视图上进行对比学习是远远不够的，因此研究异构跨视图对比机制对于HGNN尤其重要
  • 如何在HIN中选择适当的视图：选择的视图应当覆盖局部和高阶结构，网络结构(schema)视图自然地捕获了局部结构，元路径视图被广泛用于提取高阶结构
  • 如何设置一个困难的对比任务：适当的对比任务能够促进学习到更具有区分度的嵌入，设计适当的对比任务对HGNN是至关重要的

该论文研究HIN上的自监督学习问题，并提出了一个新的使用共同对比学习(co-contrastive learning)异构图神经网络HeCo

2.相关工作

异构图神经网络：HAN, MAGNN, GTN, HGT, HetGNN, HSNE

对比学习：DGI, GMI, MVGRL, GCC, DMGI

3.预备知识

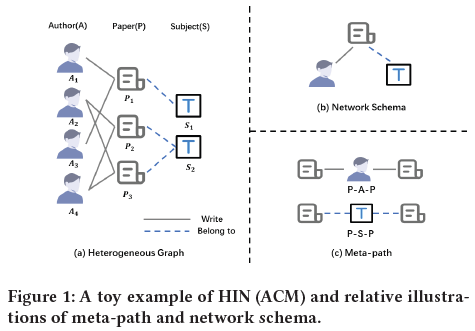
定义3.1 异构信息网络(HIN) 异构信息网络定义为一个网络G=(V, E)，以及顶点类型映射φ: V→A和边类型映射ψ: E→R，A和R分别表示顶点类型集合和边类型集合，|A|+|R|>2

定义3.2 网络结构(Network Schema) 异构信息网络G的网络结构 $T_G=(A, R)$ 是G的元模板，顶点类型是顶点，边类型是边

定义3.3 元路径(metapath) 元路径P定义为具有以下形式的路径： $A_1 \xrightarrow{R_1} A_2 \xrightarrow{R_2} \cdots \xrightarrow{R_{l-1}} A_{l}$ （简写为 $A_1A_2 \cdots A_l$），其中Ai∈A, Ri∈R，描述了顶点类型A1和Al之间的一个复合关系 $R=R_1 \circ R_2 \circ \cdots \circ R_{l-1}$

异构图示例

4.HeCo模型

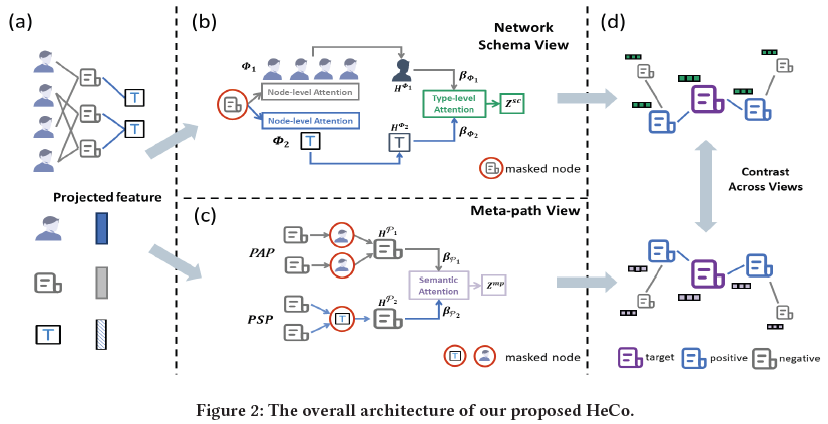
整体架构图如图2所示

模型结构

4.1 顶点特征转换

首先将不同类型顶点的特征映射到相同的隐含向量空间，如图2(a)所示

对于φi类型的顶点i，对其特征xi进行以下变换：

公式(1)

其中 $h_i \in R^d$

4.2 网络结构视图引导的编码器

这一步的目标是学习顶点i在网络结构视图下的嵌入，如图2(b)所示

假设目标顶点i关联了S种类型的顶点 $\lbrace\Phi_1, \cdots ,\Phi_S\rbrace$ ，顶点i的 $\Phi_m$ 类型的邻居定义为 $N_i^{\Phi_m}$

对于顶点i，不同类型的邻居，以及同种类型的不同邻居对其嵌入有不同的贡献，因此在顶点层次和类型层次应用注意力机制来从不同类型的邻居聚集信息

具体地，首先应用顶点层次的注意力来混合 $\Phi_m$ 类型的邻居：

公式(2)

其中 $\alpha_{i,j}^{\Phi_m}$ 表示 $\Phi_m$ 类型的邻居j对顶点i的注意力值，计算方式如下：

公式(3)

得到所有类型的嵌入 $\lbrace h_i^{\Phi_1}, \cdots ,h_i^{\Phi_S}\rbrace$ 后，利用类型层次的注意力将它们混合起来得到最终嵌入 $z_i^{sc}$ ，即顶点i在网络结构视图下的嵌入

公式(4)

$\beta_{\Phi_m}$ 表示类型 $\Phi_m$ 对顶点i的重要性 最后加权求和

公式(5)

这部分与HAN基本相同，只是将元路径改为邻居类型

4.3 元路径视图引导的编码器

这一步的目标是学习顶点i在元路径（高阶结构）视图下的嵌入，如图2(c)所示

假设顶点i关联了M条元路径 $\lbrace P_1, \cdots ,P_M\rbrace$ ，顶点i基于元路径 $P_n$ 的邻居定义为 $N_i^{P_n}$

每条元路径表示了一种语义相似度，应用元路径相关的GCN来编码这一特征：

公式(6)

其中di是顶点i的度（根号其实就是归一化的邻接矩阵 $D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$）

M条元路径可以得到顶点i的M个嵌入 $\lbrace h_i^{P_1}, \cdots ,h_i^{P_M}\rbrace$ ，之后利用语义层次的注意力将它们混合起来得到最终嵌入 $z_i^{mp}$ ，即顶点i在元路径视图下的嵌入

公式(8)

$\beta_{P_n}$ 表示元路径 $P_n$ 对顶点i的重要性

最后加权求和

公式(7)

这部分将HAN顶点层次的注意力中的GAT改为了GCN，语义层次的注意力与HAN完全相同

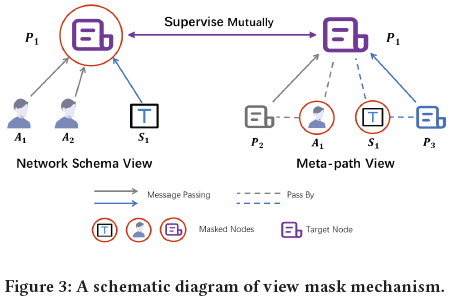
4.4 视图mask机制

在生成 $z_i^{sc}$ 和 $z_i^{mp}$ 的过程中，该论文设计了一种视图mask机制，分别隐藏网络结构视图和元路径视图不同的部分

具体地，在图3的示例中，P1是目标顶点

在网络结构编码的过程中，P1只聚集了邻居A1, A2和S1，而屏蔽了来自它自己的信息；而在元路径编码的过程中，消息只从P2和P3沿元路径PAP和PSP传播到P1，而丢弃了中间顶点A1和S1的信息

因此P1的两个嵌入是相关但互补的，可以相互监督训练，这展示了一种协同趋势

（这就叫设计了一种机制？）

视图mask机制

4.5 协同对比优化

从以上两个视图得到 $z_i^{sc}$ 和 $z_i^{mp}$ 之后，将其输入两层MLP，映射到计算对比损失的空间：

公式(9)

注意两个视图的MLP的参数是共享的

接下来需要定义HIN中的正负样本

给定网络结构视图下的一个顶点，可以简单地定义其元路径视图下的嵌入为正样本，但是考虑到顶点之间是通过边相关联的，因此该论文提出了一种新的正样本选择策略：如果两个顶点被很多元路径关联，则它们是正样本，如图2(d)所示，这种策略的优点是选择出的正样本可以很好地反映目标顶点的局部结构

对于顶点i和j，定义函数 $C_i(j)$ 表示这两个顶点之间的元路径数量：

公式(10)

构造一个集合 $S_i=\lbrace j \vert j \in V \; and \; \mathbb{C}_i(j) \ne 0\rbrace$ 并按Ci(j)的值降序排序 之后设置一个阈值 $T_{pos}$ ，如果 $\vert S_i \vert >T_{pos}$ 则从 $S_i$ 选择前 $T_{pos}$ 个顶点作为顶点i的正样本，即为 $\mathbb{P}_i$；否则保留 $S_i$ 中的所有顶点 自然地将所有剩余顶点视为i的负样本，即为 $\mathbb{N}_i$

有了正负样本集合，网络结构视图下的对比损失如下 ： 公式(11)

其中sim(u, v)表示余弦相似度，τ表示温度参数

与传统对比损失的区别是这里考虑了多个正样本对

示例：顶点数N=3，正样本矩阵 $P=\begin{pmatrix}1&0&1 \newline 0&1&0 \newline 0&1&1\end{pmatrix}$ ， $P_{ij}=1$ 表示j是i的正样本

相似度函数 $s_{ij}=\exp(\cos(z_i^{sc}\_proj,z_j^{mp}\_proj))$ ，则

\[\mathcal{L}_0^{sc}=-\log \frac{s_{00}+s_{02}}{s_{00}+s_{01}+s_{02}}, \mathcal{L}_1^{sc}=-\log \frac{s_{11}}{s_{10}+s_{11}+s_{12}}, \mathcal{L}_2^{sc}=-\log \frac{s_{21}+s_{22}}{s_{20}+s_{21}+s_{22}}\]

注：对比学习的方法最早来自MoCo和SimCLR（计算机视觉领域），原始的对比损失公式为

\[l(i,j)=-\log \frac{\exp(sim(z_i,z_j)/\tau)}{\sum_{k=1}^N \exp(sim(z_i,z_k)/\tau)}\]

其中(i, j)是一对正样本

从该公式可以看出对比损失本质上就是交叉熵损失，相当于样本i的标签为j、预测概率为 $sim(z_i,z_j)/\tau$ ，之后softmax

另外，实际上“正样本”并不是原样本集合中的两个样本，而是每一个原样本 $x_i$ 经过两种不同的数据增强变换得到的两个新样本互为正样本，假设这两个新样本经过编码得到的向量分别为 $y_i$ 和 $z_i$ ，则相似度为 $sim(y_i,z_i)$

注意到目标顶点i的嵌入来自网络结构视图，而正/负样本的嵌入来自元路径视图，这就实现了跨视图自监督

另一个对比损失 $\mathcal{L}_i^{mp}$ 类似，只是目标顶点i的嵌入来自元路径视图，而正/负样本的嵌入来自网络结构视图

整体目标函数如下：

公式(12)

最终使用 $z^{mp}$ 进行下游任务，因为目标类型的顶点显式参与到了 $z^{mp}$ 的生成中（没懂）

4.6 模型扩展

更加困难的负样本对于对比学习是非常重要的，因此该论文提出了使用新的负样本生成策略的两种扩展模型

HeCo_GAN 基于GAN网络，使用生成器生成高质量负样本

HeCo_MU 基于MixUp模型，混合困难的负样本生成更难的负样本

5.实验

5.1 实验设置

数据集

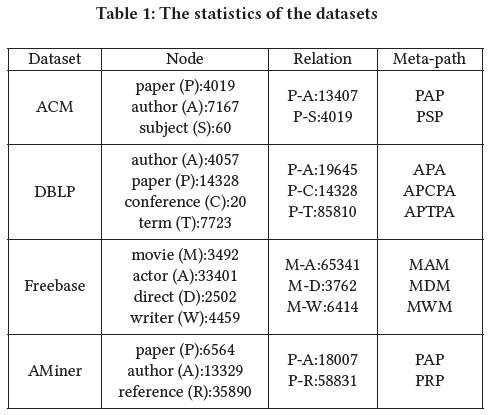
数据集

（又是这些小规模数据集）

  • ACM：论文3分类
  • DBLP：学者4分类
  • Freebase：电影3分类
  • AMiner：论文4分类

Baseline

  • 无监督同构方法：GraphSAGE, GAE, DGI
  • 无监督异构方法：metapath2vec, HERec, HetGNN, DMGI
  • 半监督异构方法：HAN

实现细节

使用Glorot初始化，Adam优化器，学习率1e-4 ~ 5e-3，注意力dropout 0.1 ~ 0.5，τ 0.5 ~ 0.9

对于元路径视图使用单层GCN，网络结构视图只考虑一跳邻居

嵌入维数64，只使用目标顶点的输入特征，其他类型的顶点使用one-hot编码

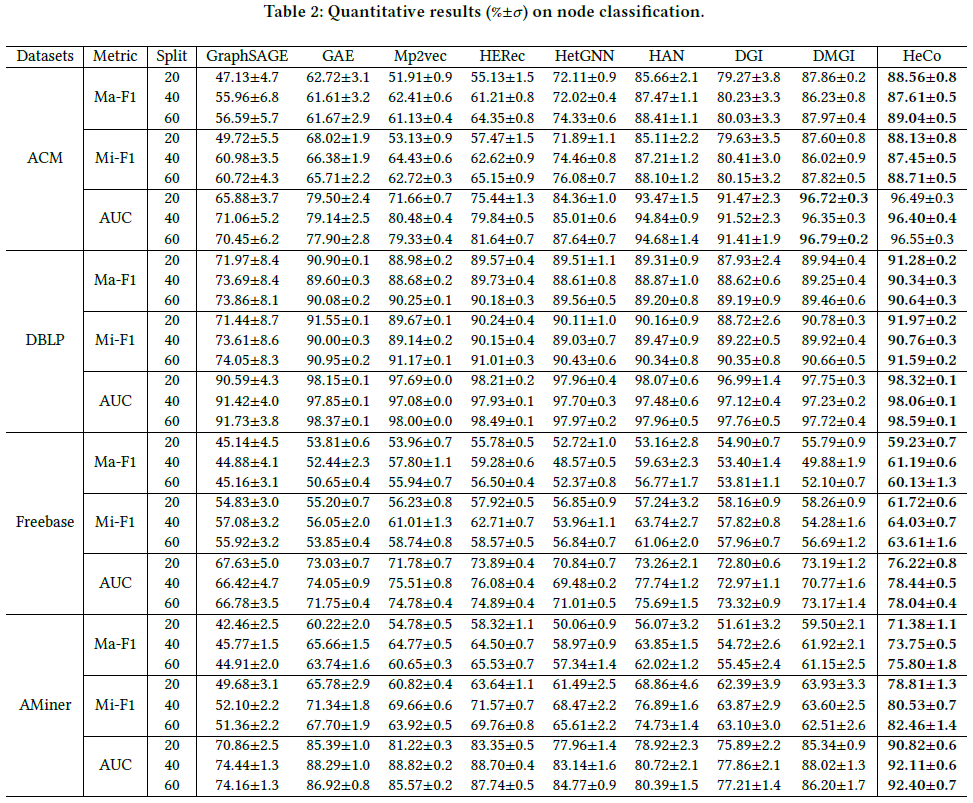
5.2 顶点分类

每个类别选择20, 40, 60个顶点作为训练集，1000个顶点作为验证集，1000个顶点作为测试集

评价指标：Macro-F1, Micro-F1, AUC

顶点分类结果

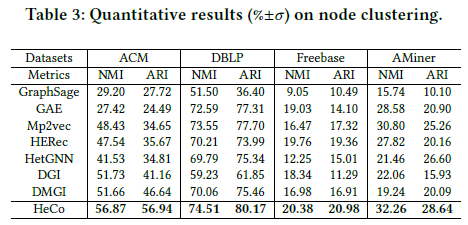
5.3 顶点聚类

在学习到的顶点嵌入上应用K-Means算法

评价指标：NMI, ARI

运行10次取平均

顶点聚类结果

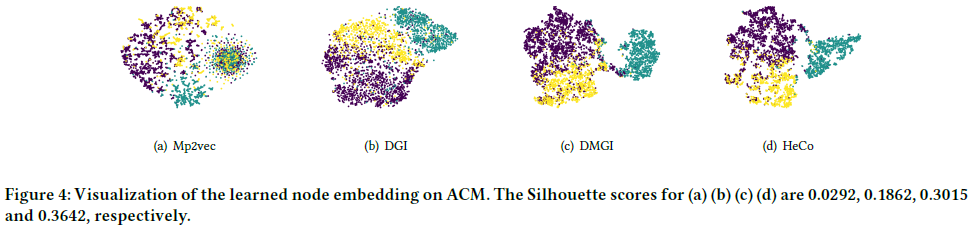
5.4 可视化

在ACM数据集上进行嵌入可视化

使用t-SNE绘制metapath2vec, DGI, DMGI和HeCo学习到的嵌入，不同颜色表示不同标签

可视化

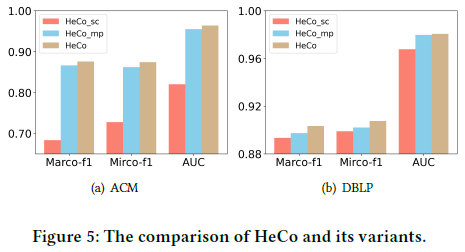
5.5 消融实验

对比HeCo的两种变体：

  • HeCo_sc：只在网络结构视图下编码顶点，对应正/负样本的嵌入来自网络结构视图
  • HeCo_mp：类似地，只在元路径视图下编码顶点

消融实验结果

Graph Neural Network
paper note heterogeneous graph neural network
This post is licensed under CC BY 4.0 by the author.