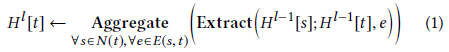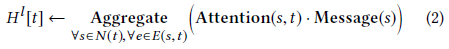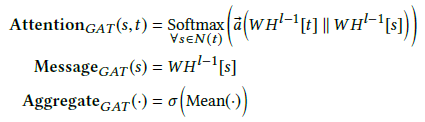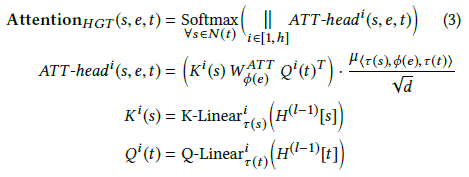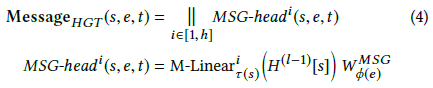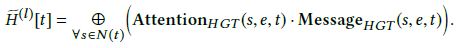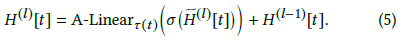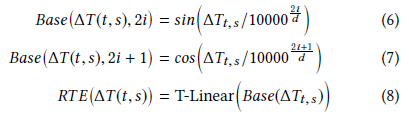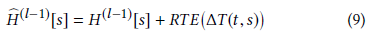Post

【论文笔记】HGT

Posted Updated
By Zhao Zhengyang 26 min read

Heterogeneous Graph Transformer

2020 WWW

论文链接：https://arxiv.org/pdf/2003.01332

代码：

1.引言

异构图的常见实例包括学术图、Facebook实体图、LinkedIn经济图、物联网网络等

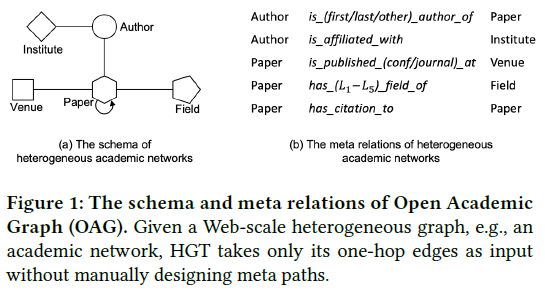
图1中的Open Academic Graph (OAG)有5种顶点：论文、学者、机构、期刊和领域

OAG网络结构

现有异构图挖掘研究存在的问题：

  • 需要为每种异构图设计元路径，需要专业领域知识
  • 要么简单地假设不同类型的节点/边共享相同的特征和表示空间，要么仅对节点类型或边类型保留不同的非共享权重，不足以捕获异构图的属性
  • 忽略了图的动态性质
  • 固有设计和实现使其无法建模Web规模（上亿级）的异构图

该论文提出了异构图Transformer(HGT)模型来解决以上问题，能够保持顶点和边类型相关的表示、捕捉网络动态性、避免自定义元路径以及能够扩展到Web规模的图

  • 为了处理图的异构性，引入了顶点和边类型相关的注意力机制：异构互注意力，该方法使用元关系三元组<起点类型, 边类型, 终点类型>来参数化用于计算注意力的权重矩阵，从而不同类型的顶点和边可以保持各自不同的表示空间，同时不同类型的顶点还可以通过消息传递进行交互。这一结构使得HGT可以通过层间消息传递结合来自不同类型的高阶邻居的信息，这可以看作“软”元路径。因此，即使HGT的输入只有一跳的边而没有人工设计的元路径，模型也能自动学习并抽取出对不同的下游任务最重要的“元路径”。
  • 为了处理图的动态性，提出了 相对时间编码(RTE) 策略，使得HGT能够学习到图的时间依赖和演化
  • 为了处理Web规模的图数据，设计了异构子图采样算法HGSampling，来进行mini-batch GNN训练，其核心思想是使采样的异构子图中不同类型的顶点具有相似的比例，同时最小化信息损失，使得模型能够在任意规模的异构图上训练和推理

该论文使用Web规模的OAG数据集，包含1.8亿顶点和20亿边，时间范围为1900~2019（史上最大规模、最长时间跨度的异构图表示学习）；此外还使用了计算机科学和医学两个特定领域的图

2.预备知识和相关工作

2.1 异构图挖掘

异构图：G=(V, E, A, R)，包括顶点和边的类型映射τ(v): V→A, φ(e): E→R

元关系(meta relation)：边e=(s, t)的元关系表示为<τ(s), φ(e), τ(t)>

元路径定义为元关系的序列

动态异构图：如果顶点s在T时刻连接到顶点t，则给边e=(s, t)赋予一个时间戳T；如果s第一次出现则也将T赋予s，s可能被赋予多个时间戳 边的时间戳是不变的，表示其创建时间（“论文→会议”边的时间戳表示论文发表在会议上的时间）；而一个顶点可以有多个时间戳（例如WWW@1994和WWW@2020表示两个不同年份的统一会议）

2.2 图神经网络

一般GNN框架：设 $H^l [t]$ 为顶点t在第l个GNN层的顶点表示，则从第l-1层到第l层的更新过程为

公式(1)

其中N(t)表示顶点t的源顶点集合，E(s, t)表示所有从s到t的边

最重要的GNN运算符是Extract()和Aggregate()（就是消息传递的消息函数和归约函数），Extract()表示邻居信息提取器，Aggregate()使用某种聚集操作（如平均、求和、最大值等）来聚集邻居（源点）信息

现有的（同构）GNN模型有GCN, GraphSAGE, GAT等

2.3 异构图神经网络

现有的异构GNN模型有RGCN, HetGNN, HAN等，但这些模型没有充分利用异构图的属性，仅使用边类型或顶点类型来决定GNN的权重矩阵

该论文考虑了参数共享，给定一条边e=(s, t)，其元关系是<τ(s), φ(e), τ(t)>，如果使用三个交互矩阵来建模对应的三个元素，则大部分权重可以被共享。例如边类型“第一作者”和“第二作者”的起点和终点类型都是“学者”到“论文”，因此关于“学者”和“论文”的知识就可以共享。

该论文将这一思想与Transformer的注意力机制结合，提出了异构图Transformer(HGT)模型

3.异构图Transformer

3.1 HGT总体架构

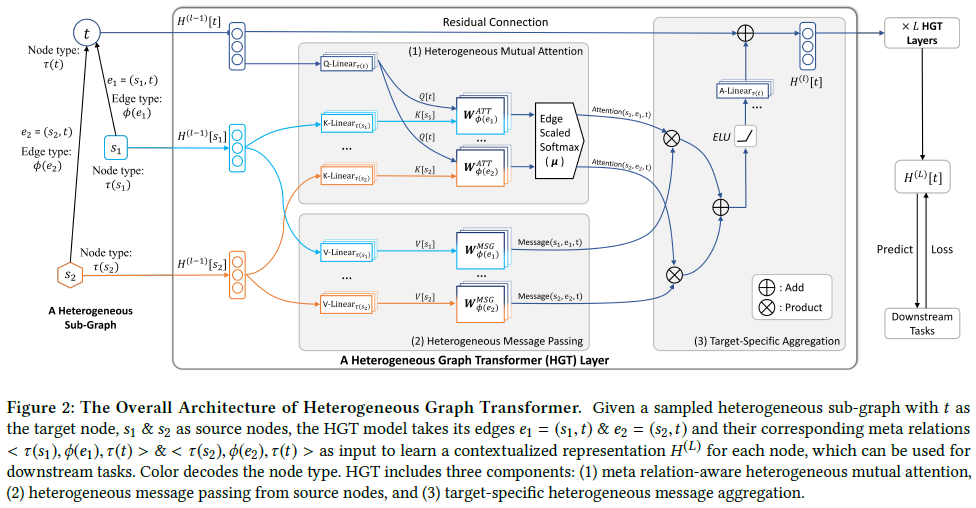
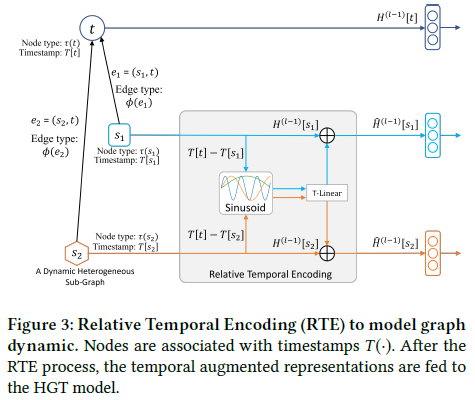
HGT的总体架构如下图所示

HGT总体架构

HGT的目标是通过聚集来自源点的信息得到每个顶点的表示，这一过程可分解为三部分：异构互注意力、异构消息传递和目标相关的聚集

将第l个HGT层的输出记为 $H^{(l)}$ ，同时也是第l+1层的输入

堆叠L层，最终的输出 $H^{(L)}$ 即为顶点表示，可用于下游任务

3.2 异构互注意力

第一步是计算源顶点s和目标顶点t之间的互注意力（图2(1)）

一般的基于注意力的GNN模型为：

公式(2)

（就是“加权求和”）

其中有三个基本的运算符：

  • Attention用于估计源顶点（邻居）s对顶点t的重要性
  • Message用于从源顶点s中提取消息
  • Aggregate使用注意力权重聚集来自邻居的消息

以GAT为例，这三个运算符分别是

GAT公式

但是GAT用于同构图，假设s和t有相同的特征分布，但在异构图中不成立

该论文设计了异构互注意力机制，给定一个目标顶点t及其所有的源顶点（邻居）s∈N(t)，目的是基于它们的元关系（即<τ(s), φ(e), τ(t)>三元组）来计算它们的互注意力

受Transformer的结构设计启发，将目标顶点t映射到一个Query向量，将源顶点s映射到一个Key向量，计算它们的点积作为注意力

具体地，对于每条边e=(s, t)计算h头注意力：

公式(3)

首先，对于第i个注意力头 ${ATT-head}^i (s, e, t)$ ，使用一个线性映射 ${K−Linear}_{\tau(s)}^i:R^d \to R^\frac{d}{h}$ 将τ(s)类型的源顶点s映射到第i个Key向量 $K^i(s)$ 。注意K-Linear的下标包含τ(s)，这意味着每种类型的顶点都有一个不同的线性映射，从而能够建模分布差异。类似地，使用一个线性映射 ${Q−Linear}_{\tau(t)}^i:R^d \to R^\frac{d}{h}$ 将目标顶点t映射到第i个Query向量 $Q^i(t)$。

接下来要计算Query向量 $Q^i(t)$ 和Key向量 $K^i(s)$ 之间的相似度。异构图的一个特点是同一个顶点类型对（τ(s)和τ(t)）之间存在多种类型的边，因此不是直接计算Query和Key向量的点积，而是为每种边类型φ(e)使用一个独立的矩阵 $W_{\phi(e)}^{ATT} \in R^{\frac{d}{h} \times \frac{d}{h}}$ ，这样模型就可以捕获同一个顶点类型对之间不同的语义关系（例如“学者”和“论文”之间的“第一作者”和“第二作者”）。另外，由于不是所有的关系都对目标顶点有同等贡献，因此增加了一个先验张量 $\mu \in R^{\vert A \vert \times \vert R \vert \times \vert A \vert}$ 来表示每种元关系的重要性。

最后，将h个注意力头拼接在一起得到每个顶点对的注意力向量。之后，对于每个目标顶点t，对所有的邻居N(t)做softmax归一化，使得 $\sum_{\forall s \in N(t)}{ATT−head}^i (s,e,t)=1$ 。

注：（个人理解）虽然HGT的注意力在形式上与Transformer的多头注意力类似，但实际上完全不同

  • Transformer的Q和K来自编码器/解码器的输出；而HGT并没有编码器/解码器结构，只有一个多头注意力，Q和K是由顶点特征乘以不同的变换矩阵（K-Linear和Q-Linear）得到
  • Transformer的注意力可以写成矩阵形式： $QK^T \in R^{N \times N}$ ；而HGT的注意力是起点（邻居）对终点的注意力，每个顶点的邻居个数不同，无法写成矩阵的形式，因此公式中都是向量形式
  • ${ATT-head}^i (s, e, t)$ 是一个数，实际就是边e上的一个特征，表示起点s对终点t的重要性，与GAT类似
  • 为什么起点特征映射到K向量、终点特征映射到Q向量？Q和K表示什么意思？→人为设计，最终目的就是计算注意力权重

3.3 异构消息传递

从源顶点到目标顶点的消息传递过程（图2(2)）和计算互注意力是并行的 对于一条边（顶点对）e=(s, t)，使用以下方式计算多头消息：

公式(4)

为了得到第i个消息头 ${MSG-head}^i (s, e, t)$ ，首先使用一个线性映射 ${M−Linear}_{\tau(s)}^i:R^d \to R^\frac{d}{h}$ （图2中是V-Linear）将τ(s)类型的源顶点s映射到第i个Message向量（图2中是V[s]）；之后乘以一个矩阵 $W_{\phi(e)}^{MSG} \in R^{\frac{d}{h} \times \frac{d}{h}}$ ；最后将h个消息头拼接起来得到边e=(s, t)上的消息 ${Message}_{HGT} (s,e,t) \in R^d$

3.4 目标相关的聚集

计算出异构多头注意力和消息后，需要将其从源顶点到目标顶点进行聚集（图2(3)）

由于公式(3)已将注意力向量归一化，因此可以将其作为权重对来自源顶点的消息取平均，得到更新后的向量 $\tilde{H}^{(l)}[t]$ ：

目标相关的聚集公式

这一步聚集了顶点t的来自不同特征分布的邻居（源顶点）的信息

最后一步是将顶点t的向量映射回其类型相关的分布，为此，使用一个线性映射 ${A−Linear}_{\tau(t)}:R^d \to R^d$ 和残差连接：

公式(5)

至此就得到了第l个HGT层的顶点t的输出，堆叠L层（L是一个很小的数）即可得到最终输出 $H^{(L)}$ ，可将其输入到任何模型来进行下游异构网络任务，例如顶点分类和连接预测

3.5 相对时间编码

这一节引入了相对时间编码(Relative Temporal Encoding, RTE)使HGT能够处理图的动态性，RTE是受Transformer的位置编码启发

相对时间编码

具体地，给定一个源顶点s和一个目标顶点t，对应的时间戳分别为T(s)和T(t)，相对时间间隔ΔT(t, s)=T(t)-T(s)作为相对时间编码RTE(ΔT(t, s))的索引

公式(6)~(8)

其中T-Linear是一个线性映射 $R^d \to R^d$

最后将相对时间编码加到顶点表示上：

公式(9)

这样得到的顶点表示可以捕获源顶点s和目标顶点t的相对时间信息

示例：设d=4, ΔT∈[0, 5)，则

\[Base=\begin{pmatrix} \sin \frac{0}{10000^0} & \cos \frac{0}{10000^\frac{1}{4}} & \sin \frac{0}{10000^\frac{2}{4}} & \cos \frac{0}{10000^\frac{3}{4}} \newline \sin \frac{1}{10000^0} & \cos \frac{1}{10000^\frac{1}{4}} & \sin \frac{1}{10000^\frac{2}{4}} & \cos \frac{1}{10000^\frac{3}{4}} \newline \sin \frac{2}{10000^0} & \cos \frac{2}{10000^\frac{1}{4}} & \sin \frac{2}{10000^\frac{2}{4}} & \cos \frac{2}{10000^\frac{3}{4}} \newline \sin \frac{3}{10000^0} & \cos \frac{3}{10000^\frac{1}{4}} & \sin \frac{3}{10000^\frac{2}{4}} & \cos \frac{3}{10000^\frac{3}{4}} \newline \sin \frac{4}{10000^0} & \cos \frac{4}{10000^\frac{1}{4}} & \sin \frac{4}{10000^\frac{2}{4}} & \cos \frac{4}{10000^\frac{3}{4}} \end{pmatrix}\]

Base可以预先计算好，使用时直接查表即可，对于任意一条边(s, t)，s的相对时间编码即为Base矩阵中ΔT(t, s)对应的行

作者代码实现：

1
2
3
4
5

position = torch.arange(0., max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, n_hid, 2) * -(math.log(10000.0) / n_hid))
emb = nn.Embedding(max_len, n_hid)
emb.weight.data[:, 0::2] = torch.sin(position * div_term) / math.sqrt(n_hid)
emb.weight.data[:, 1::2] = torch.cos(position * div_term) / math.sqrt(n_hid)

其中max_len表示ΔT的取值范围是[0, max_len)， $position=\begin{pmatrix} 0 \newline 1 \newline \vdots \newline max\_len-1 \end{pmatrix}$ 表示ΔT的各个取值， $divterm=\begin{pmatrix} \frac{1}{10000^0} & \frac{1}{10000^\frac{2}{d}} & \cdots & \frac{1}{10000^\frac{d-2}{d}} \end{pmatrix}$ 表示偶数列sin里边的分母部分，二者相乘是一个max_len*d/2的矩阵，表示偶数列sin里边的值，最后偶数列再取sin即可，奇数列同理

注：

  • 代码中奇数列cos里边的部分也使用了position * div_term，即cos里边的分母并不是(2i+1)/d而是2i/d
  • div_term第2i项为 $\frac{1}{10000^\frac{2i}{d}}=10000^{-\frac{2i}{d}}=e^{-\frac{2i}{d}\ln 10000}$
  • 代码中在计算完sin和cos之后还除以了维数的平方根，但公式中并没有体现

4.Web规模的HGT训练

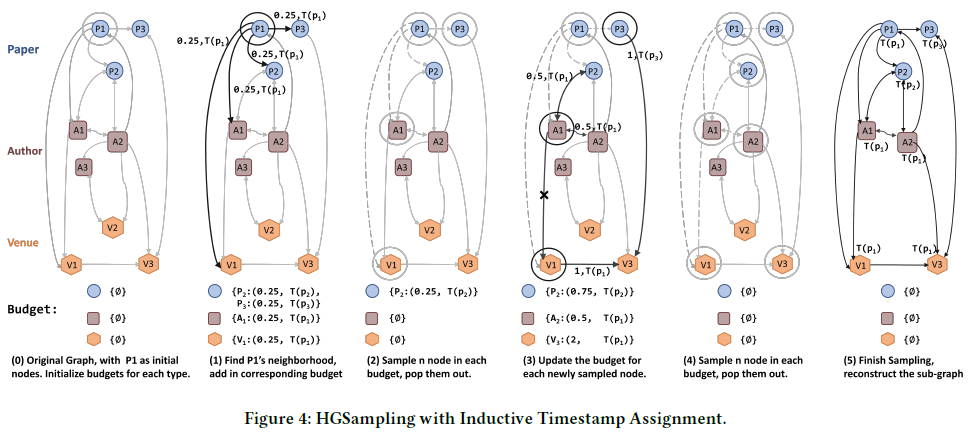
4.1 HGSampling

为了解决Web规模（超大规模）的GNN难以训练，以及现有基于采样的方法在异构图上导致子图不均衡的问题，该论文提出了异构子图采样算法HGSampling，该算法能够为每种类型保留相似数量的节点和边，以及使采样的子图保持密集，以最小化信息损失并减少样本方差

HGSampling示意图

算法1

HGSampling的流程如算法1所示，其基本思想是为每个顶点类型τ维护一个预算B[τ]，并使用重要性采样策略每种类型采样相等数量的顶点来减小方差

给定已采样的顶点t，使用算法2将其所有直接邻居添加到对应的预算中，并在第8行将t的归一化的度加到这些邻居，之后用于计算采样概率

算法2

更新预算后，在算法1的第9行计算采样概率，在每个预算中计算每个顶点s的累积归一化度的平方，使用这样的采样概率可以减小采样方差

之后，第11行使用计算出的概率采样n个τ类型的顶点，第12~15行将这些顶点添加到输出顶点集合，将其邻居更新到预算中，并将其从预算中删除

重复这一过程L次可得到一个距初始顶点深度为L的采样子图，最后重建被采样顶点之间的邻接矩阵

4.2 归纳式时间戳分配

普通顶点(plain nodes)不与固定的时间关联，需要赋予不同的时间戳，例如会议顶点

事件顶点(event nodes)有显式关联的时间戳，例如论文顶点

该论文提出了归纳式时间戳分配算法，用于基于普通顶点关联的事件顶点来赋予其时间戳

该算法体现在算法2的第6行，其思想是普通顶点从事件顶点继承时间戳（就这么简单。。）

5.评价

5.1 Web规模的数据集

实验使用的数据集是Open Academic Graph (OAG)，包含1.78亿顶点和22.36亿边，是最大的公开学术数据集，其中每篇论文都关联了发表日期，从1900年到2019年

另外还构造了两个特定领域的子图：计算机科学(CS)和医学(Med)，也都包含几千万顶点和几亿边，比其他学术数据集（例如DBLP和Pubmed）至少大一个数量级

数据集

共有5种类型的顶点：P, A, F, V, I分别表示论文、学者、领域、期刊和机构顶点

OAG中的领域分6级L0~L5，被组织为层次树状结构，“论文-领域”边也分为相应的等级

另外，“学者-论文”边区分作者顺序（第一作者、最后一个作者和其他），“论文-期刊”边区分类型（期刊、会议和预印本），”Self”边表示自环连接（GNN模型通常都会添加）

除”Self”关系外，每种边类型φ都有一个逆关系 $φ^{-1}$

5.2 实验设置

任务和评价

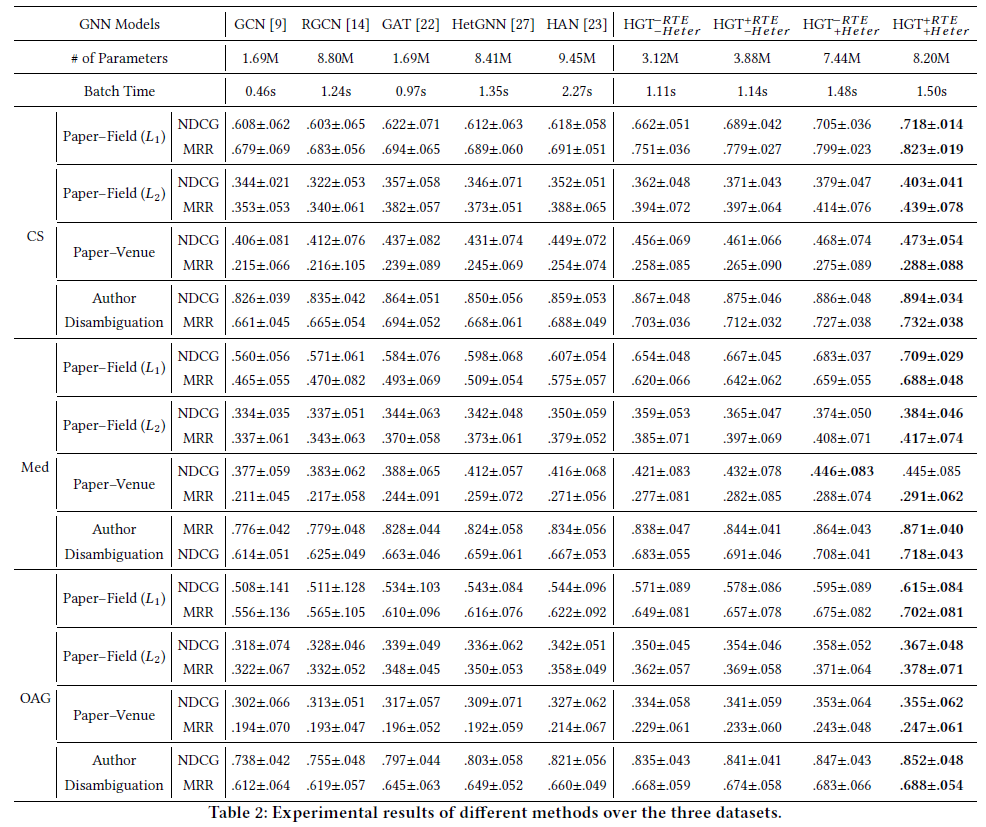
论文中在4个真实世界的下游任务上评价HGT模型：预测论文-领域(L1)、论文-领域(L2)、论文-期刊，以及学者消歧

前3个顶点分类任务的目标是预测论文所属的L1领域、L2领域或发表的期刊，使用不同的GNN来获得顶点表示，使用一个softmax输出层来获得类标签

对于学者消歧，选择所有同名的作者及其关联的论文，任务是进行这些论文和候选学者之间的连接预测，从GNN获得顶点表示后，使用一个神经张量网络来获得“学者-论文”对应该被连接的概率

对于所有的任务，使用2015年之前的论文作为训练集，2015~2016年的论文作为验证集，2016~2019年的论文作为测试集

使用NDCG和MRR作为评价指标

所有的模型都是训练5次，取测试性能的均值和标准差

Baseline

HGT和所有Baseline均使用PyG实现

同构图GNN：

  • GCN
  • GAT 异构图GNN：
  • RGCN
  • HetGNN
  • HAN

消融实验

HGT的两个主要部分：异构权重参数化(Heter)和相对时间编码(RTE)

为了研究这两个部分的影响，论文中进行了消融研究，”-Heter”表示给所有元关系赋予相同的权重，”-RTE”表示不加相对时间编码，共比较4种变体： ${HGT}_{−Heter}^{−RTE},{HGT}_{−Heter}^{+RTE},{HGT}_{+Heter}^{−RTE},{HGT}_{+Heter}^{+RTE}$

输入特征

对于论文，使用预训练的XLNet得到论文标题中每个单词的表示，之后以每个单词的注意力为权重取平均得到论文的输入特征

学者的输入特征即为其论文特征的平均

对于领域、期刊和机构，使用metapath2vec预训练的顶点嵌入作为输入特征

由于同构图GNN假设顶点特征属于相同的分布，而论文中提取的输入特征不满足这一假设（论文和学者顶点的特征是词向量，其他顶点特征是metapath2vec预训练的嵌入向量），为了公平，在将特征输入到GNN之前，还对每种类型的顶点进行不同的线性映射，将不同类型的顶点特征映射到相同的分布

实现细节

隐藏层维数为256，注意力头数为8，GNN均为3层

AdamW优化器，Cosine Annealing学习率调度器，200 epoch

5.3 实验结果

实验结果

Graph Neural Network
paper note heterogeneous graph neural network
This post is licensed under CC BY 4.0 by the author.