《C++程序设计原理与实践》笔记第6章编写一个程序

Posted Oct 16, 2022 Updated Sep 19, 2024

By Zhao Zhengyang 38 min read

接下来的两章将从一个最初不清晰的想法开始，经过分析、设计、实现、测试、再设计、再实现等步骤开发一个计算器程序，目的是帮助读者了解在编写代码的过程中如何去思考。在这个过程中将讨论程序结构、用户定义类型和输入处理。

6.1 一个问题

编写程序往往从一个问题开始，即你有一个问题，想要一个程序来帮助解决。因此理解问题是编写好程序的关键。

我们编写一个简单计算器，即“让计算机对输入的表达式做常规的算术运算”。例如，输入 “2+3.1*4” ，程序应该输出 “14.4” 。

6.2 对问题的思考

我们如何开始？总的来说，需要思考一下这个问题以及如何解决它。

首先，考虑程序应该做什么，以及如何与它交互
之后，考虑如何编写程序来实现这样的功能

要记住，本章和下一章实现程序最终版本的过程（提出部分解、产生想法和发现错误的历程）与程序最终版本同样重要，甚至比语言技术细节更重要。

6.2.1 程序开发的阶段

解决一个问题需要反复经历以下阶段：

分析(analysis)：弄清应该做什么，并给出对当前问题理解的描述，称为需求规格说明书(software requirements specification)（属于软件工程的范畴，本书不详细讨论，但问题的规模越大就越重要）。
设计(design)：给出系统的整体结构图，并确定实现包括哪些部分以及这些部分之间如何相互联系。
实现(implementation)：编写代码、调试和测试，确保程序完成预期的功能。

6.2.2 策略

下面是一些对很多程序设计项目都有帮助的建议：

要解决的问题是什么？此时应该站在用户而不是程序员的角度，考虑程序要实现什么功能，而不是如何实现。
- 一开始不要过于有野心，更好的方式是将问题简化，使程序易于定义、理解和实现，一旦程序可以工作，基于已有的经验可以实现“2.0版本”。
- 时间、技巧和工具等资源是否足够？
将程序分解为多个可处理的部分。
- 有哪些工具、库或其他辅助手段？
- 寻找可以独立描述的部分解决方案，或许能用在程序中的多个地方，甚至其他程序中（可复用）。
实现一个小的、有限的程序来解决问题的关键部分，称为原型程序(prototype)，目的是：
- 找出我们的理解、思想和工具中存在的问题
- 看看能否改变问题描述的一些细节使其更加容易理解
实现一个完整的解决方案。理想情况是逐步构建组件来编写一个程序，而不是一次性写完所有代码。

6.3 回到计算器问题

如何与计算器交互？很简单：使用cin和cout，即键盘和控制台窗口。从键盘输入表达式，计算结果并写出到屏幕上。例如：

Expression: 2+2
Result: 4
Expression: 2+2*3
Result: 8
Expression: 2+3-25/5
Result: 0

像这种如何使用程序的示例称为用例(use case)。

程序的主要逻辑可用伪代码(pseudo code)描述如下：

  
read_a_line
calculate    // do the work
write_result

6.3.1 初次尝试

下面编写一个计算器的最初版本：

简单计算器v0

程序的基本思想是：先读取最左边的操作数，之后每次读取一个运算符和其右操作数，并执行相应的运算，例如：2*3-8+7=((2*3)-8)+7=(6-8)+7=-2+7=5。程序能够运行，但存在以下几个问题：

按从左到右的顺序计算，忽略了运算符的优先级，例如输入 “1+2*3” 时输出结果是 “9” 而不是正确结果 “7” （逻辑错误）
不支持输入浮点数，并且只能做整数除法
没有处理除数为0的情况
一次只能读取一个表达式

注：书中本章剩余部分的介绍顺序有些混乱，不太容易理解（尤其是对于没有编译原理背景知识的读者），下面按照比较容易理解的方式重新组织一下。

6.3.5 重新开始

为了解决优先级问题，我们必须“向前看”这一行有没有*或/，因此必须调整这种简单的从左到右的计算顺序。然而，尝试这样做会立刻遇到很多困难：

如何处理分散在多行的表达式？
如何在数字之间搜索运算符？
如何记住运算符的位置？
如何处理不按从左到右顺序的计算？（例如 “1+2*3” 、 “1+2*3+4” 、 “1+2*3/4%5+(6-7*(8))” 等）

这些问题使用“简单方法”是无法解决的，初学者可能很难想出解决方案。实际上，要解决这些问题，需要用到文法。

可以支持变量吗？例如v=7; m=9; v*m;——好主意，不过先放一放，还是先实现计算器的基本功能。在7.8节将会看到，如果决定实现变量功能，代码量将会是原来的两倍。在项目早期避免功能蔓延(feature creep)是很重要的。相反，应该先构建一个简单版本，只实现最基本的功能。一旦程序能够运行，就可以添加更多功能。分阶段构建一个程序比一次完成要简单得多。

6.4 文法

6.4.0 基本概念

注：文法来自于形式语言与自动机，是一种很有用的工具，也是编译原理的基础理论。书中并未介绍这些基本概念，对于初学者来说也有些抽象，但是了解这些基本概念对于理解本章后面的内容很有帮助。

文法(grammar)定义为四元组G = (V, T, P, S)，其中

V为非终结符(non-terminal symbol)集合
T为终结符(terminal symbol)集合
P为产生式规则(production rule)集合，每个产生式具有以下形式：$A \to \alpha$ ，其中 $A \in V, \alpha \in (V \cup T)^*$
- 同一个非终结符的多个产生式 $A \to \alpha_1, A \to \alpha_2, …, A \to \alpha_n$ 可简写为 $A \to \alpha_1 \vert \alpha_2 \vert … \vert \alpha_n$
$S \in V$ 为开始符号(start symbol)

对于文法G = (V, T, P, S)，设 $\alpha, \beta, \gamma \in (V \cup T)^*, A \in V$ ，如果 $A \to \gamma$ 是G的产生式，则称 $\alpha A \beta$ 可派生或推导出 $\alpha \gamma \beta$，记作 $\alpha A \beta \Rightarrow \alpha \gamma \beta$.

设 $\alpha, \beta \in (V \cup T)^*$，如果α经过若干步可以推导出β，则记为 $\alpha \stackrel{*}{\Longrightarrow} \beta$.

文法G = (V, T, P, S)产生的语言(language)记为 $L(G) = \lbrace w \vert w \in T^*, S \stackrel{*}{\Longrightarrow} w\rbrace$，即开始符号S可以推导出的所有终结符串的集合。

示例

示例1 文法 $G = (\lbrace S\rbrace , \lbrace a\rbrace , \lbrace S \to a \vert aS\rbrace , S)$ 产生的语言是所有由n个a组成的字符串(n ≥ 1)，即 $L(G) = \lbrace a^n \vert n \ge 1\rbrace $.

例如：$S \Rightarrow aS \Rightarrow aaS \Rightarrow aaa$，其中前两步推导使用了产生式 $S \to aS$，最后一步使用了 $S \to a$. 空串、aab不属于该文法产生的语言.

示例2 文法 $G = (\lbrace S\rbrace , \lbrace a, b\rbrace , \lbrace S \to \epsilon \vert aSb\rbrace , S)$ 产生的语言是所有由n个a和n个b组成的字符串，包括空串（用ε表示），即 $L(G) = \lbrace a^nb^n \vert n \ge 0\rbrace $.

例如：$S \Rightarrow aSb \Rightarrow aaSbb \Rightarrow aaaSbbb \Rightarrow aaabbb$，其中前三步推导使用了产生式 $S \to aSb$，最后一步使用了 $S \to \epsilon$.

示例3 文法 $G = (\lbrace S, A, B\rbrace , \lbrace a, b\rbrace , \lbrace S \to AB, A \to aA \vert a, B \to bB \vert b\rbrace , S)$ 产生的语言是所有由m个a和n个b组成的字符串(m, n ≥ 1)，即 $L(G) = \lbrace a^mb^n \vert m, n \ge 1\rbrace $.

注：以上几个简单示例的终结符都是单个字符，实际上也可以是一个字符串，只要将其视为一个整体即可。书中下面两节给出了两个更加实际的例子。

6.4.1 英文文法

下面是英文文法的一个很小的子集（使用双引号表示终结符）：

G = (V, T, P, Sentence)
V = {Sentence, Noun, Verb, Conjunction}
T = {"birds", "fish", "C++", "rules", "fly", "swim", "and", "or", "but"}

产生式规则如下：
Sentence:
    Noun Verb
    Sentence Conjunction Sentence
Conjunction:
    "and"
    "or"
    "but"
Noun:
    "birds"
    "fish"
    "C++"
Verb:
    "rules"
    "fly"
    "swim"

以下句子属于该文法产生的语言：

birds fly but fish swim
C++ rules
C++ fly and birds rules

注：虽然最后一个句子从自然语言的角度是没有意义的，甚至存在（英文）语法错误，但从形式语言的角度它严格符合文法G的产生式规则，因此对文法G来说是一个合法的“句子”。

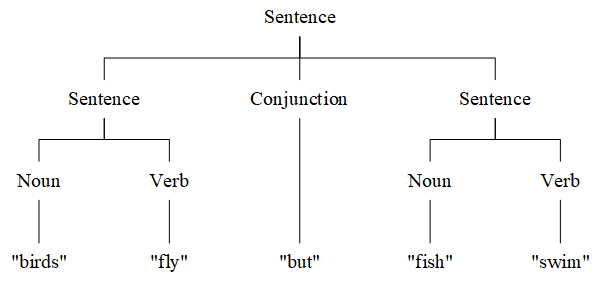
语法分析树(parse tree)使用树的形式来表示推导过程，根节点对应开始符号，非叶节点对应非终结符，叶节点对应终结符，父子关系对应产生式规则。

语法树和推导是等价的，从上往下即为推导(derivation)，从下往上即为归约(reduction)。

例如，对于上面的文法，句子 “birds fly but fish swim” 的语法分析树如下：

6.4.2 设计一个文法

文法的产生式规则是如何设计出来的？最诚实的回答是“经验”。

下面是一个列表的文法：

G = (V, T, P, List)
V = {List, Sequence, Element}
T = {"{", "}", ",", "A", "B"}

产生式规则如下：
List:
    "{" Sequence "}"
Sequence:
    Element
    Element "," Sequence
Element:
    "A"
    "B"

下面这些是List：

{A}
{B}
{A,B}
{A,A,A,A,B}

下面这些不是List：

{}
A
{A,A,A,A,B
{A,A,C,A,B}
{A B C}
{A,A,A,A,B,}

计算器表达式文法

回到计算器问题，6.3.5节遇到的问题可以通过表达式文法来解决：

G = (V, T, P, Expression)
V = {Expression, Term, Primary, Number}
T = {float-literal, "+", "-", "*", "/", "%", "(", ")"}

产生式规则如下：
Expression:
    Term
    Expression "+" Term
    Expression "-" Term
Term:
    Primary
    Term "*" Primary
    Term "/" Primary
    Term "%" Primary
Primary:
    Number
    "(" Expression ")"
Number:
    float-literal

注意：终结符float-literal比较特殊，除了类别外还有值，因此使用(kind, value)对表示。

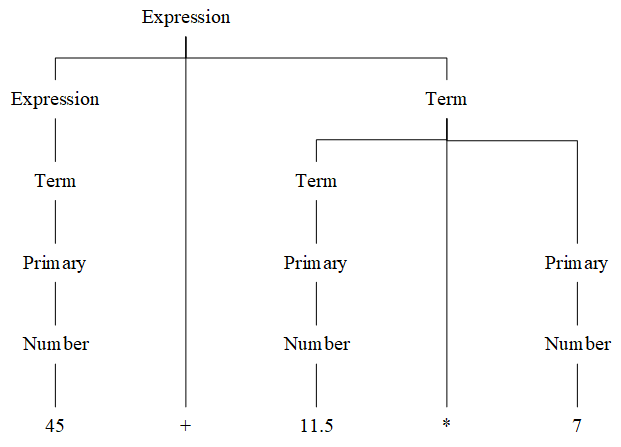
例如，表达式 “45+11.5*7” 的语法分析树如下：

如何使用文法

利用文法可以将文本字符串构造成一棵语法分析树，包括以下两个步骤：

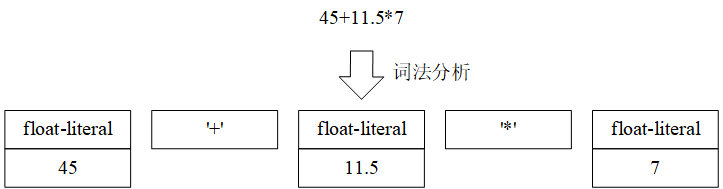
词法分析(lexical analysis)：将输入字符（源代码）转换为终结符序列（如下图所示），负责词法分析的程序称为词法分析器(lexer)
语法分析(syntax analysis/parse)：按照产生式规则将终结符序列构造成语法分析树（如上图所示），负责语法分析的程序称为语法分析器(parser)

文法是如何解决6.3.5节遇到的问题的：

如何处理计算顺序（优先级）：设计产生式规则，使得*和+位于语法分析树的不同层次
如何记住数字和运算符的位置：通过语法分析的递归过程
如何处理多行表达式：通过词法分析忽略空白符

简单计算器程序的词法分析将在6.3.3和6.8节介绍，语法分析将在6.5节介绍（书中在6.3.1节发现优先级问题之后就引入了Token，但并没有解决这一问题，让人无法理解为什么要引入这一概念；6.4节才介绍文法，6.8节才给出真正的词法分析器实现，反而在6.5节先给出了语法分析器的实现，令人迷惑）。

注：

在编译原理中，编程语言的语法就是使用文法定义的（例如C++17标准（附录A）、Java 8语法、Python 3语法、Go语法），词法分析和语法分析就是编译器的主要工作过程。
计算器使用的表达式语法本质上就是一种小型的编程语言。
在真正的语法分析器中，并不需要真的把语法分析树构造出来，只需确定如何从终结符序列一步步归约为开始符号，并执行每一步归约所使用的产生式对应的语义动作即可。对于计算器程序，语义动作即为执行算术运算；对于C++编译器，语义动作即为生成汇编指令。
《C程序设计语言》第5章 “复杂声明”一节就使用了文法。

6.3.2 单词

单词(token)就是终结符，在简单计算器程序中使用(kind, value)对表示；词法分析过程称为分词(tokenize)，即读取输入字符并组合为单词。

首先，定义一个类型Token来表示单词。类型(type)或者类(class)的作用是保存需要的数据，并提供对这些数据的操作。例如，int类型保存整数，并提供加、减、乘、除、取模等算术运算；string类型保存字符序列，并提供拼接、下标等操作。除了内置类型和标准库提供的类型，C++还允许用户自定义类型(user-defined type)。

6.3.3 实现单词

Token类的定义如下：

Token类

Token是一个类，它有两个数据成员(data member) kind和value。关键字class表示用户自定义类型，可以包含零个或多个成员（类似于变量），用于保存数据。可以像这样使用Token：

  
Token t;              // 默认值
t.kind = '+';         // 成员访问
cout << t.kind;       // 成员访问
Token t2{'8', 3.14};  // 初始化
Token t3 = t;         // 拷贝初始化
t = t2;               // 拷贝赋值

注：C++的类和C语言的结构体类似，但C++类/结构体的初始化可以不带等号，而C结构体的初始化带等号。

使用成员访问运算符 . 来访问成员：对象名.成员名。类的公有成员可以像普通变量一样访问和赋值。

用户自定义类型除了数据成员外还可以有成员函数(member function)，用于提供对数据成员的操作，见9.4.2和9.7节。

6.3.4 使用单词

要实现计算器程序的词法分析器，需要一个能够读取输入并返回下一个单词的函数，下面通过另一个类型Token_stream来实现这一功能。

注：没有必要一次性将全部输入读取到一个Token向量。实际上，词法分析和语法分析是同时进行的：语法分析器调用词法分析器，一边读取单词，一边归约产生式并执行语义动作（见6.5节）。

6.8 单词流

在cin读取一个int时，在没有读到非数字字符之前，无法判断当前读入的整数是否完整（例如，读取到123时，有可能是在读入12345，也可能是123+456），因此最终会多读取一个字符。这个多读取的字符（例如 ‘+’）必须被放回到输入流中，否则该字符将丢失，下次读取一个char时读到的将是 ‘4’ 而不是 ‘+’。

类似地，词法分析器在读取单词序列时，有时也需要多读取一个单词才能判断当前属于哪个产生式。例如，对于表达式 “1+2+3” 和 “1+2*3”，当读取到单词 “2” 时，无法判断应该计算加法还是继续读取，因为这取决于下一个单词是 “+” 还是 “*” 。

因此，我们需要一个类似于标准输入流的“单词流”，负责处理单词的读取和放回，这就是Token_stream：

Token_stream类

注：Token_stream类充当了计算器程序的词法分析器。

C++的类通常由两部分组成：公共接口（用public:标识）和实现细节（用private:标识）：

  
class Foo {
public:
    // user interface
private:
    // implementation details
};  // don't forget ';'!

公共接口应该只包含用户需要的内容，通常是一组函数；实现细节包括用于处理复杂细节的数据和函数，用户不必知道也不应该直接使用。

类的公有成员和函数在任何地方都可以访问，而私有成员和函数只能被该类的成员和友元访问（一个类的对象也可以访问同一个类其他对象的私有成员）。

Token_stream类定义了两个公有函数，对应其两个主要功能：

get()：从输入中读取字符，并从中构造出单词
putback()：放回一个单词

这两个名字与标准库istream类对应功能的函数是一致的。在系统中保持命名的一致性是比较重要的，有助于记忆和避免错误。

6.8.1 实现Token_stream

由于计算器程序至多只会多读取一个单词，因此每次至多只会放回一个单词。因此，只需要声明能够存放一个单词的缓冲区成员buffer和标识缓冲区空或满的bool型成员full。实现如下：

Token_stream类实现

注：为了方便测试，还增加了一个istream成员，表示用于读取输入的输入流，并通过构造函数参数传递，这样不仅可以从cin读取，还可以从文件(ifstream)或字符串(istringstream)读取。另外，使用自定义异常类Lexer_error表示词法分析器的错误（类似于5.6.1节中的Bad_area）。

为了保持代码清晰，一般在类定义中声明数据成员和成员函数（放在头文件中），而在类外定义成员函数（放在源文件中）。在类外定义成员时，需要使用语法 类名::成员名 指定成员所属的类。

构造函数(constructor)是一种特殊的成员函数，用于初始化成员，其名称与类型相同，没有返回值。另外，构造函数的参数表和函数体之间可以有一个可选的成员初始化列表：:成员1(初值1), 成员2(初值2), ...，详见Constructors and member initializer lists。这里full(false)将成员full初始化为false，buffer{0}将成员buffer初始化为kind和value都是0（注：这种大括号初始化语法是C++11引入的列表初始化）。

成员函数putback()比较简单，只需将放回的单词拷贝到buffer，并将full置为true即可。在此之前，需要先检查缓冲区中是否已经有单词，如果有则抛出Lexer_error异常。

真正的词法分析工作由get()函数完成，该函数返回输入中的下一个单词(kind, value)，下面详细分析该函数。首先检查缓冲区中是否已经有单词，如果有则直接返回，并将full置为false；如果没有，则从输入中读取一个字符：

对于括号和运算符，一个字符就构成了一个单词，单词的kind就是该字符本身，没有value
对于数字或小数点，将第一个字符放回cin，然后使用cin的>>运算符读取整个数字，作为单词的value，并使用一个特殊值'8'（定义为常量number）作为kind
另外还增加了两个单词：;表示打印结果，q表示退出
对于任何其他（非法）字符，抛出Lexer_error异常

注：

读取数值的判断条件是以数字或小数点开头，因此并不支持负数。
cin也支持putback()操作，用于将已经读入的第一个字符（数字或小数点）放回输入流（cin的缓冲区），这里如果不放回，读取到的数值将是不完整的。
这里直接使用cin完成数值的读取，省去了复杂的工作——这就是编程的精髓：不断寻找更简单的方法，即“优秀的程序员都是懒惰的”。

6.5 将文法转换为代码

下面实现语法分析器，即根据文法的产生式规则解析单词序列。

6.5.1 实现文法规则

将文法规则转换为语法分析器代码的方法有很多种，最简单的一种方式是递归下降语法分析，其基本思想是：

为每个非终结符编写一个可递归调用的处理函数
函数体按产生式的右端来编写，当遇到终结符时直接匹配，当遇到非终结符时就调用相应的处理函数

例如，6.4.2节中的列表文法对应的语法分析器伪代码如下：

List() {
    t1 = get_token()  // "{"
    s = Sequence()
    t2 = get_token()  // "}"
    return t1 + s + t2
}

Sequence() {
    e = Element()
    t = get_token()
    if (t == ",") {
        return e + t + Squence()
    }
    else {
        putback(t)
        return e
    }
}

Element() {
    return get_token()  // "A" or "B"
}

6.5.2 Expression

对于计算器的表达式文法，需要为非终结符Expression、Term和Primary分别编写一个处理函数。但是该文法存在左递归：Expression -> Expression "+" Term，该产生式对应的代码为：

Expression() {
    e = Expression()  // 无限递归！
    op = get_token()  // "+"
    t = Term()
    return e + t
}

这将导致无限递归，因此必须先消除左递归。

分析一下表达式文法，可以看出Expression实际上是一个Term后面跟着若干个"+" Term或"-" Term，即Expression -> Term ("+" Term | "-" Term)*，从而可以将递归转换为循环。

因此，Expression的处理函数可以先读取一个Term，之后读取一个运算符，如果是+或-则再读取一个Term并执行相应的运算，重复这一过程，直到遇到其他运算符。伪代码如下：

Expression() {
    t = Term()
    op = get_token()
    while (op == "+" or "-") {
        if (op == "+")
            t += term()
        else
            t -= term()
        op = get_token()
    }
    putback(op)  // 注意放回！
    return t
}

注意：当遇到+或-之外的单词时需要将其放回，否则该单词将丢失，导致后续解析错误。

6.5.3 Term

Term的处理函数与Expression非常类似，其产生式可转换为Term -> Primary ("*" Primary | "/" Primary)*（取模运算%将在7.5节实现），注意处理除数为0的情况。

6.5.4 Primary

Primary的产生式不存在左递归，只需判断两种情况：首先读取一个单词

如果是(，则读取一个Expression和)，如果缺少右括号则抛出Parser_error异常
如果是数字则直接返回
其他情况抛出Parser_error异常

伪代码如下：

Primary() {
    t = get_token()
    if (t == '(') {
        e = Expression()
        if (get_token() != ')')
            error()
        return e
    }
    else if (t == number)
        return t.value
    else
        error()
}

下面是语法分析器的完整实现：

语法分析器

注：

由此可以看出，词法分析和语法分析是同时进行的，语法分析器一边调用词法分析器读入单词，一边计算表达式的值。
为了便于测试，将三个处理函数封装在Parser类中，并将Token_stream作为其成员，而不是像书中代码一样使用一个全局变量。另外，使用自定义类型Parser_error表示语法分析器的错误。

6.6 试验第一个版本

main()函数比较简单，只需调用parser.expression()并打印结果即可：

主程序

下面是程序运行结果：

8;
=8
1+2*3;
=7
1 - 2
*3+4
;
=-1
1-34/50;
=0.32
42+(11-4)/8-9*(32.5+24.7);
=-471.925
q
primary expected

可以看出，第一个版本的计算器程序已经基本可以正常工作了，但仍然存在几个问题：

q命令的处理位置不正确：最后输入q并不是在if (t.kind == 'q')中退出，而是调用parser.expression()时抛出异常退出，除非最后一个表达式不输入;（将在7.3节解决）
不支持负数（将在7.4节解决）
不支持取模运算%（将在7.5节解决）
没有错误恢复：发生错误时程序会立刻终止（将在7.7节解决）

6.9 程序结构

书中给出的程序结构将所有类和函数放在一个源文件中。实际上，按照词法分析、语法分析和主程序可以很自然地拆分为两个头文件和三个源文件，如下图所示：

6.9.1 编译

按照上面划分源文件的方式，可以使用以下命令编译得到可执行文件：

g++ -o calculator_v1 main.cpp lexer.cpp parser.cpp  # 编译+链接

该命令一次性完成了编译和链接。虽然只需要一条命令，但是当任何一个源文件发生变化时都需要重新编译三个源文件。另一种方式是分别执行编译和链接命令：

  
g++ -c -o lexer.o lexer.cpp  # 编译
g++ -c -o parser.o parser.cpp  # 编译
g++ -c -o main.o main.cpp  # 编译
g++ -o calculator_v1 main.o lexer.o parser.o  # 链接

这里分别将三个源文件(.cpp)编译为对象文件(.o)，最后将三个对象文件链接成可执行文件(calculator_v1)。这样当某个源文件发生变化时，只需执行编译该文件的命令和链接命令即可，未发生变化的源文件不需要重新编译。

习题

C/C++, PPP

cpp grammar

This post is licensed under CC BY 4.0 by the author.