《C++程序设计原理与实践》笔记 第21章 算法和映射

本章将完成我们对STL基本思想及其所提供的功能的介绍。本章重点关注算法。

21.1 标准库算法

标准库提供了大约80种算法。本章重点关注一些最常用的算法：

算法	功能
find(b, e, v)	返回v在[b, e)中首次出现的位置
find(b, e, p)	返回[b, e)中使得p(x)为true的第一个元素的位置
count(b, e, v)	返回v在[b, e)中出现的次数
count_if(b, e, p)	返回[b, e)中使得p(x)为true的元素个数
sort(b, e)	使用<对[b, e)排序（升序排序）
sort(b, e, p)	使用p对[b, e)排序
copy(b, e, b2)	将[b, e)拷贝到[b2, b2+(e-b))，b2之后应当有足够的空间
unique_copy(b, e, b2)	将[b, e)拷贝到[b2, b2+(e-b))，不拷贝相邻的重复元素
merge(b, e, b2, e2, r)	将两个有序序列[b, e)和[b2, e2)合并至[r, r+(e-b)+(e2-b2))
equal_range(b, e, v)	返回有序序列[b, e)中值为v的子序列，本质上是对v的二分搜索
equal(b, e, b2)	判断[b, e)和[b2, b2+(e-b)的所有元素是否相等
accumulate(b, e, i)	返回i与[b, e)中所有元素的和
accumulate(b, e, i, op)	类似于accumulate，但使用op代替+
inner_product(b, e, b2, i)	返回[b, e)和[b2, b2+(e-b))的内积
inner_product(b, e, b2, i, op, op2)	类似于inner_product，但使用op和op2代替+和*

标准库算法定义在头文件<algorithm>和<numeric>中。默认情况下，相等比较使用==（例如find()、count()和equal()），而排序是基于<（例如sort()）。输入序列由一对迭代器定义；输出序列由指向首元素的迭代器定义（假定后面有足够的空间）。所有算法都是函数模板，迭代器类型和元素类型作为模板参数。通常，数值算法由一个或多个操作参数化（例如accumulate()和inner_product()），这些操作定义为函数或函数对象（见21.4节）。查找算法通常通过返回输入序列的结尾来表示“失败”（例如，find(b, e, v)如果未找到v则返回e）。

21.2 最简单的算法：find()

最简单但有用的算法是find()，它在序列中查找给定值：

template<class InputIt, class T>
InputIt find(InputIt first, InputIt last, const T& value) {
    while (first != last && *first != value)
            ++first;
    return first;
}

注：上面的定义暗含了对于模板参数InputIt和T的语义要求（见19.3.2节）：（1）InputIt支持!=、*和++操作，即输入迭代器；（2）InputIt的*运算符返回类型可转换为T；（3）T类型支持!=比较。

我们可以像这样使用find()：

void f(vector<int>& v, int x) {
    auto p = find(v.begin(), v.end(), x);
    if (p != v.end()) {
        // we found x in v
    }
    else {
        // no x in v
    }
    // ...
}

find()定义中的循环是简洁高效的，并且是基本算法的直接表示。另一种实现方式如下：

template<class InputIt, class T>
InputIt find(InputIt first, InputIt last, const T& value) {
    for (; first != last; ++first)
        if (*first == value)
            return first;
    return last;
}

这两种定义在逻辑上是等价的。

21.2.1 一些泛型用法

find()算法是泛型的，这意味着它可以被用于不同的数据类型，包括任何STL风格的序列、任何元素类型。

下面是一些例子：

// works for vector of int
void f(vector<int>& v, int x) {
    auto p = find(v.begin(), v.end(), x);
    if (p != v.end()) { /* we found x */ }
    // ...
}

在这里，InputIt = vector<int>::iterator，T = int。++first是移动指针，*first是指针解引用，first != last是比较两个指针，而*first != value是比较两个整数。

下面尝试list：

// works for list of string
void f(list<string>& v, const string& x) {
    auto p = find(v.begin(), v.end(), x);
    if (p != v.end()) { /* we found x */ }
    // ...
}

在这里，InputIt = list<string>::iterator，T = string。++first是沿着Link::succ指针到下一个元素，*first是访问Link::val，first != last是比较两个Link*，而*first != value是比较两个string。

因此，find()是相当灵活的：只要遵循了迭代器的简单规则，我们就可以使用find()来查找任何序列和容器的元素。例如，可以使用find()在20.6节定义的Document中查找字符：

// works for Document of char
void f(Document& v, char x) {
    Text_iterator p = find(v.begin(), v.end(), x);
    if (p != v.end()) { /* we found x */ }
    // ...
}

注：find()也可用于内置数组：

// works for vector of int
void f(int a[], int n, int x) {
    auto p = find(a, a + n, x);
    if (p != a + n) { /* we found x */ }
    // ...
}

在这里，InputIt = int*，T = int。

这种灵活性是STL算法的特点，使其更加有用。

21.3 通用搜索：find_if()

通常，我们不是查找一个特定值，而是查找满足某些条件的值。例如，查找大于42的值、奇数值、包含字母x的字符串、地址字段是 “17 Cherry TreeLane” 的记录等。

基于用户提供的条件进行搜索是算法是find_if()：

template<class InputIt, class Pred>
InputIt find(InputIt first, InputIt last, Pred p) {
    for (; first != last; ++first)
        if (p(*first))
            return first;
    return last;
}

显然，find_if()与find()很像，除了返回条件是p(*first)而不是*first == value。

其中p是一个一元谓词(unary predicate)，即接受一个参数、返回布尔值的函数（注：“p是一元谓词”这一要求隐含在find_if()的实现中，模板参数Pred不包含任何约束）。可以使用函数、Lambda表达式或函数对象（见21.4节）作为谓词。例如，我们可以这样查找int向量中的第一个奇数：

bool odd(int x) { return x % 2; }  // % is the modulo operator

void f(vector<int>& v) {
    auto p = find_if(v.begin(), v.end(), odd);
    if (p != v.end()) { /* we found an odd number */ }
    // ...
}

上面的find_if()将对每个元素调用odd()，直到找到第一个奇数。注意，这里直接将函数名作为参数，实际上是作为函数指针(pointer to function)传递，模板参数Pred = bool (*)(int)（见《C程序设计语言》笔记 第5章 指针与数组 5.11节）。

类似地，我们可以查找list中第一个大于42的值：

bool larger_than_42(double x) { return x > 42; }

void f(list<double>& v) {
    auto p = find_if(v.begin(), v.end(), larger_than_42);
    if (p != v.end()) { /* we found a value > 42 */ }
    // ...
}

21.4 函数对象

我们希望向find_if()传递的谓词能够将元素与通过参数指定的值进行比较：

void f(list<double>& v, int n) {
    auto q = find_if(v.begin(), v.end(), Larger_than(n));
    if (q != v.end()) { /* we found a value > n */ }
    // ...
}

显然，Larger_than必须满足：

• 能够像函数一样调用（例如Larger_than(n)(*first)）
• 能够存储一个值（例如n）

为此，我们需要函数对象(function object)。函数对象是指重载了函数调用运算符()的对象，从而能够像函数一样被调用。例如函数指针、Lambda表达式、std::function对象，以及任何重载了operator()的自定义类型的对象。例如：

Larger_than函数对象

Larger_than(n)(x)等价于x > n，其中Larger_than(n)调用构造函数，(x)以及find_if()中的p(*first)调用Larger_than::operator()。运算符()叫做函数调用运算符(function call operator)或应用运算符(application operator)，其参数列表可以是任意的。

参考：

• Function call operator
• Function objects
• Pointers to functions
• named requirement FunctionObject
• C++函数式编程

21.4.1 函数对象的抽象视角

函数对象提供了一种通用的、强大的、方便的机制，允许“函数”携带它所需的数据。考虑函数对象更一般的概念：

// abstract example of a function object
class F {
public:
    F(const S& ss) :s(ss) { /* establish initial state */ }
    T operator()(const S& ss) const {
        // do something with ss to s
        // return a value of type T (T is often void, bool, or S)
    }

    const S& state() const { return s; }  // reveal state
    void reset(const S& ss) { s = ss; }   // reset state

private:
    S s;  // state
};

类F的对象通过其成员s存储数据（“状态”）。F::operator()只接受一个参数，但我们可以定义具有任意多个参数的函数对象。

函数对象的使用是STL主要的参数化方法。例如，使用函数对象指定find_if()的查找规则、sort()的排序规则、accumulate()的算术操作等。函数对象的使用是灵活性和通用性的主要来源。

21.4.2 类成员上的谓词

标准算法能够正确处理基本类型的元素序列。然而类对象的容器更为常见。考虑一个对很多应用领域都很关键的示例，根据几个标准对记录进行排序：

struct Record {
    string name;    // standard string for ease of use
    char addr[24];  // old style to match database layout
    // ...
};

vector<Record> vr;

有时需要按姓名排序，有时又需要按地址排序。幸运的是，我们能够简单、高效地实现：

sort(vr.begin(), vr.end(), Cmp_by_name());  // sort by name
sort(vr.begin(), vr.end(), Cmp_by_addr());  // sort by addr

其中，函数对象Cmp_by_name()按name比较两个Record，Cmp_by_addr()按addr比较两个Record。标准库算法sort()可以接受第三个参数，使用户能够指定比较标准。Cmp_by_name()创建了一个Cmp_by_name对象。

注：标准排序算法sort()有两个重载：

template<class RandomIt>
void sort(RandomIt first, RandomIt last);

template<class RandomIt, class Compare>
void sort(RandomIt first, RandomIt last, Compare comp);

其中，RandomIt是随机访问迭代器（这意味着不能用于list），Compare是二元谓词。第一种形式对序列[first, last)中的元素按升序排序，即使用运算符<比较元素；第二种形式使用comp比较元素，如果comp(a, b)为true，则a排在b之前。

下面定义Cmp_by_name和Cmp_by_addr：

// different comparisons for Record objects:
struct Cmp_by_name {
    bool operator()(const Record& a, const Record& b) const
        { return a.name < b.name; }
};

struct Cmp_by_addr {
    bool operator()(const Record& a, const Record& b) const
        { return strncmp(a.addr, b.addr, 24) < 0; }  // !!!
};

Cmp_by_name直接使用string的<运算符比较name字符串。而addr既不是string，也不是C风格字符串，而是长度为24的字符数组（非0结尾）。因此Cmp_by_addr使用了C标准库头文件<string.h>中的函数strncmp()。

21.4.3 Lambda表达式

在程序中定义一次性使用的函数或函数对象（例如odd()、larger_than_42()、Larger_than和Cmp_by_name）有点繁琐。在这种情况下，可以使用Lambda表达式（15.3.3节）。例如：

sort(vr.begin(), vr.end(),  // sort by name
    [](const Record& a, const Record& b) { return a.name < b.name; }
);
sort(vr.begin(), vr.end(),  // sort by addr
    [](const Record& a, const Record& b) { return strncmp(a.addr, b.addr, 24) < 0; }
);

对于21.4节中find_if()的例子，也可以使用Lambda表达式：

void f(list<double>& v, int n) {
    auto p = find_if(v.begin(), v.end(), [](int x) { return x > 42; });
    if (p != v.end()) { /* we found a value > 42 */ }

    auto q = find_if(v.begin(), v.end(), [n](int x) { return x > n; });
    if (q != v.end()) { /* we found a value > n */ }
    // ...
}

注：实际上，对于带捕获的Lambda表达式，编译器会生成一个匿名类。详见C++函数式编程 第5节。

21.5 数值算法

头文件<algorithm>中的标准库算法大多都是处理数据：拷贝、排序、搜索等。而数值算法处理数值计算。例如：

数值算法	功能
accumulate(b, e, i)	累加，返回i+b[0]+b[1]+…+b[n-1]
inner_product(b, e, b2, i)	内积，返回i+b[0]b2[0]+b[1]b2[1]+…+b[n-1]*b2[n-1]
partial_sum(b, e, r)	部分和，输出序列b[0], b[0]+b[1], …, b[0]+b[1]+…+b[n-1]，保存到r
adjacent_difference(b, e, r)	相邻差，输出序列b[0], b[1]-b[0], …, b[n-1]-b[n-2]，保存到r
iota(b, e, i)	整数序列，将序列[b, e)填充为i, i+1, …, i+n-1

这些算法定义在头文件<numeric>中。本节将介绍前两个。

21.5.1 accumulate()

最简单、最有用的数值算法是accumulate()。该算法累加序列中的值：

template<class InputIt, class T>
T accumulate(InputIt first, InputIt last, T init) {
    for (; first != last; ++first)
        init = init + *first;
    return init;
}

例如：

int a[] = {1, 2, 3, 4, 5};
int sum = accumulate(a, a + 5, 0);

vector<double> v = {1.1, 2.2, 3.3, 4.4};
double sum2 = accumulate(v.begin(), v.end(), 0.0);

sum = 0 + 1 + 2 + 3 + 4 + 5 = 15, sum2 = 0.0 + 1.1 + 2.2 + 3.3 + 4.4 = 11.0。

注意，结果类型与初始值init的类型相同。

21.5.2 一般化accumulate()

基本的accumulate()使用加法。然而，我们可能还需要对序列进行累乘。为此，STL提供了四个参数版本的accumulate()，我们可以指定要使用的操作：

template<class InputIt, class T, class BinaryOperation>
T accumulate(InputIt first, InputIt last, T init, BinaryOperation op) {
    for (; first != last; ++first)
        init = op(init, *first);
    return init;
}

其中op可以是任何二元操作。例如：

vector<double> v = {1.1, 2.2, 3.3, 4.4};
double product = accumulate(v.begin(), v.end(), 1.0, multiplies<double>());

product = 1.0 × 1.1 × 2.2 × 3.3 × 4.4 = 35.1384。这里使用的二元运算符multiplies<double>()是实现乘法的标准库函数对象，multiplies<double>()(x, y)等价于x * y。还有其他的二元函数对象：plus（加法）、minus（减法）、divides（除法）、modulus（取模）等，定义在<functional>中。

如sort()的例子（21.4.2节）一样，我们通常对类对象中的数据更感兴趣，而不仅仅是基本类型。例如，给定物品的单价和数量，我们希望计算总价：

计算物品总价

21.5.3 inner_product()

两个向量的内积(inner product)是对应位置的元素相乘，并将所有结果相加。即：

\[\mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^n a_i b_i\]

下面是STL版本：

template<class InputIt1, class InputIt2, class T>
T inner_product(InputIt1 first1, InputIt1 last1, InputIt2 first2, T init) {
    while (first1 != last1) {
        init = init + (*first1) * (*first2);
        ++first1;
        ++first2;
    }
    return init;
}

这将内积的概念推广到任何类型元素的任何序列。以股票市场指数为例，选择一组公司，并给每个公司赋予一个“权重”。为了获得当前指数的值，需要将每个公司的股票价格与其权重相乘，并将所有结果相加。显然，这是价格和权重的内积。例如：

计算股票市场指数

注意，inner_product()接受两个序列，但是只有三个参数：第二个序列只有开始位置。第二个序列的元素应该至少和第一个序列一样多，否则将产生运行时错误（越界访问）。对于inner_product()来说，第二个序列的元素可以多于第一个序列，“多余的”元素将不会被处理。

两个序列不需要是相同的类型，也不需要具有相同的元素类型（只要可以相乘即可）。为了说明这一点，我们使用vector来保存价格而使用list保存权重。

21.5.4 一般化inner_product()

inner_product()也可以像accumulate()一样一般化。对于inner_product()，需要两个额外的参数：一个用于组合累加器和新值（对应“加法”），一个用于组合元素值对（对应“乘法”）：

template<class InputIt1, class InputIt2, class T, class BinaryOperation1, class BinaryOperation2>
T inner_product(
        InputIt1 first1, InputIt1 last1,
        InputIt2 first2, T init,
        BinaryOperation1 op1, BinaryOperation2 op2) {
    while (first1 != last1) {
        init = op1(init, op2(*first1, *first2));
        ++first1;
        ++first2;
    }
    return init;
}

在21.6.3节，我们将回到这个例子，使用一般化的inner_product()作为更优雅的解决方案。

21.6 关联容器

除了vector外，最有用的标准库容器可能就是map。映射(map)是一个键值对(key, value)的序列，可以基于键(key)来查找值(value)。在标准库中，将这类数据结构统称为关联容器(associative container)。

标准库提供了8种关联容器：

关联容器	数据结构	key有序	key唯一	底层实现
map	映射	√	√	红黑树
set	集合	√	√	红黑树
unordered_map	映射	×	√	散列表
unordered_set	集合	×	√	散列表
multimap	映射	√	×	红黑树
multiset	集合	√	×	红黑树
unordered_multimap	映射	×	×	散列表
unordered_multiset	集合	×	×	散列表

这些容器定义在<map>、<set>、<unordered_map>和<unordered_set>中。

21.6.1 map

考虑一个简单的任务：统计一段文本中的单词出现次数。最明显的方式是维护一个单词列表以及每个单词已经出现过的次数。读取一个新的单词时，首先判断是否已经见过。如果是，则将计数加1；否则将其插入到列表中，并赋值为1。我们可以使用vector或list实现，但这样每读取一个单词就要进行一次查找，这会非常慢。相反，在map中查询一个key非常容易：

统计单词出现次数

其中，words是一个string到int的映射。换句话说，给定一个string，可以访问对应的int。

map的[]运算符访问key对应的value，因此words[s]是字符串s对应的int的引用。如果s不存在，则先执行插入，value为int类型的默认值0。

程序中真正有趣的部分是++words[s]：对于读取的新单词s，如果在words中不存在，则words[s]会插入一个键值对(s, 0)，之后++将value加1；如果s已存在，则++直接将对应的value加1。从而这一个表达式就表达了单词计数的核心思想。

接下来要生成输出。我们可以遍历一个map，就像其他STL容器一样。map<string, int>的元素类型是pair<string, int>（即键值对），pair的两个成员分别叫做first和second（分别对应key和value）。

小结

map常用操作：

• map<K, V> m = { {key1, value1}, {key2, value2}, ... }; 从初始化列表构造
• m[key] 返回key对应的value的引用，如果key不存在则先执行插入，value为类型V的默认值
• m[key] = value 将key映射到value，如果key已存在则覆盖原有值
• m.at(key) 返回key对应的value的引用，如果key不存在则抛出out_of_range异常
• m.at(key) = value 将key映射到value并覆盖原有值，如果key不存在则抛出out_of_range异常
• m.size() 返回键值对个数
• m.find(key) 查找指定的key并返回迭代器，如果不存在则返回m.end()
• m.count(key) 返回指定key的出现次数（对于map只能是0或1）
• m.contains(key) (C++20)判断指定的key是否存在
• m.insert(make_pair(key, value))或m.emplace(key, value) 插入(key, value)，如果已存在则不插入
• m.erase(key) 删除指定的key
• m.lower_bound(key) 返回第一个不小于key的元素的迭代器
• m.upper_bound(key) 返回第一个大于key的元素的迭代器
• m.equal_range(key) 返回等于key的范围的起止迭代器

注意：[]运算符可能会执行插入操作，因此不是const成员函数，不能用于const map！

遍历：

• for (const auto& p : m) 按key的顺序遍历m，其中p的类型是const pair<K, V>&
• for (const auto& [k, v] : m) 按key的顺序遍历m，其中[k, v]是C++17引入的结构化绑定语法，k和v的类型分别是const K&和const V&

21.6.2 map概览

STL map的实现通常是平衡二叉搜索树(binary search tree)，更具体地说是红黑树(red-black tree)。

注：《C程序设计语言》笔记 第6章 结构 6.5节就介绍了二叉搜索树。

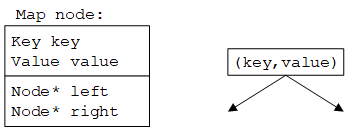
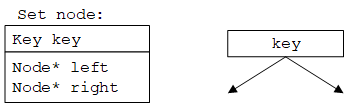
树(tree)是由节点(node)组成的数据结构，每个节点包含(key, value)对、指向左子树的指针和指向右子树的指针，如下图所示。

二叉搜索树的性质：左子树所有节点的key均小于根节点，右子树所有节点的key均大于根节点，即对于任意节点满足left->key < key < right->key（value不参与排序）。

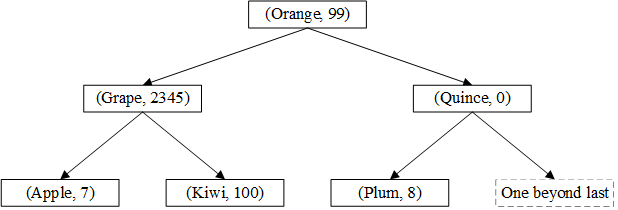
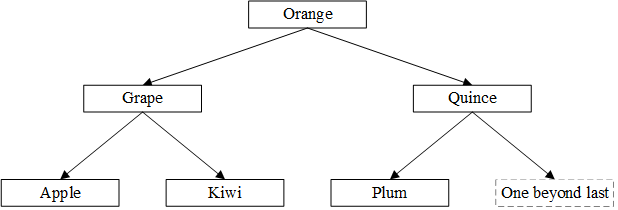
下面是一个map<string, int>的内存示意图，假设已经插入了(Kiwi,100), (Quince,0), (Plum,8), (Apple,7), (Grape,2345)和(Orange,99)：

根据以上性质，在二叉搜索树中查找一个给定key的算法如下：

bool search(root, key) {
    if (root == nullptr)
        return false
    if (key == root.key)
        return true
    else if (key < root.key)
        return search(root.left, key)
    else
        return search(root.right, key)
}

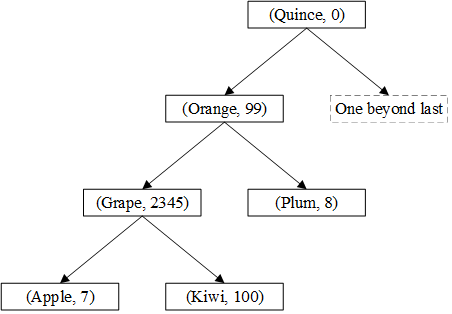
如果一棵树的左右子树的节点数大致相等，则这棵树是平衡的。如果一棵具有N个节点的树是平衡的，则查找一个key至多需要查询 $\log_2 N$ 个节点，这比线性数据结构（vector和list）平均N/2次查找要好得多（但是左右子树的指针占用了更多的内存，即用空间换时间）。

例如，上图中的树是平衡的，下图中的树是不平衡的（但它仍然满足二叉搜索树的性质）：

用于实现标准库map的树是平衡的（红黑树，一种平衡二叉搜索树）。

标准库map的接口如下：

template<class Key, class Value, class Compare = less<Key>>
class map {
public:
    using key_type = Key;
    using mapped_type = Value;
    using value_type = pair<const Key, Value>;  // a map deals in (Key,Value) pairs
    using iterator = ...;   // similar to a pointer to a tree node

    iterator begin();   // points to first element
    iterator end();     // points one beyond the last element
    
    Value& operator[](const Key& k);    // subscript with k
    iterator find(const Key& k);        // is there an entry for k?
    iterator erase(iterator p);         // remove element pointed to by p
    pair<iterator, bool> insert(const value_type& value);    // insert a (key,value) pair
    // ...
};

注意：

• 第三个模板参数Compare用于比较节点的key。
• value_type并不是Value，而是键值对pair<const Key, Value>。
• 可以将map迭代器想象成Node*，其元素类型（即*运算符的返回类型）是value_type，即迭代map时的元素是键值对。
• 迭代map时，将按key的顺序访问元素。

pair是另一个有用的STL类型，定义在<utility>中：

// simplified version of std::pair
template<class T1, class T2>
struct pair {
    using first_type = T1;
    using second_type = T2;

    pair(const T1& x, const T2& y) :first(x), second(y) {}
    // ...

    T1 first;
    T2 second;
};

template<class T1, class T2>
pair<T1, T2> make_pair(T1 x, T2 y) {
    return {x, y};
}

21.6.3 另一个map示例

为了更好地理解map的用途，我们回到21.5.3节股票市场指数的例子。只有当价格和权重在向量中的位置一一对应时，这段代码才是正确的。解决这个问题的一种方法是使用映射将公司代号与权重放在一起，例如(“AA”, 2.4808)。类似地，将公司代号与股票价格放在一起(“AA”, 34.69)。即通过相同的key将两个映射中的value关联起来。

计算股票市场指数v2

注：这种方法的前提仍然是dow_price和dow_weight的key集合相同，否则计算内积时会将两个不同公司的价格和权重相乘。另外，dow_name[symbol]默认symbol在dow_name中存在，否则会自动插入(symbol, "")。

使用map而不是vector的原因：

• 需要显式地在不同的值之间建立联系。
• map查找更快（如果不需要value，可以使用set）。
• map的key是有序的。

21.6.4 unordered_map

使用find()在vector中查找一个元素，需要从头开始逐个访问元素，平均代价与vector的长度N成正比，我们称时间复杂度为 $O(N)$ 。

要在map中查找一个元素（使用[]运算符或map::find()），需要从根节点开始向下查找，平均代价与树的高度成正比。具有N个节点的平衡二叉树的高度为 $\log_2 N$ ，即时间复杂度为 $O(\log_2 N)$ ——这与 $O(N)$ 相比好得多。

注意，时间复杂度仅描述算法的时间代价随问题规模的增长趋势，实际代价还与具体实现方式有关。例如，在vector中顺序访问元素通常比在map中沿指针访问节点更快。

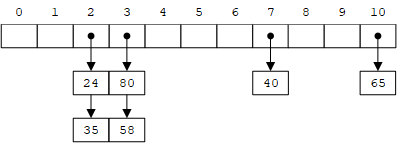
对于某些类型，特别是整数和字符串，散列表/哈希表(hash table)比二叉搜索树查找更快。散列表通常使用数组实现，数组的每个位置叫做一个桶(bucket)。核心思想是：给定一个key，计算散列值/哈希值(hash value)并对数组长度取模，从而直接得到桶索引：

\[f(k) = hash(k) \% D\]

其中hash是散列函数，D是数组长度。

注：《C程序设计语言》笔记 第6章 结构 6.6节就介绍了散列表。

例如，假设key是整数，$hash(k) = k, D = 11$，则插入80, 40, 65, 58, 24, 35之后的散列表如下图所示。如果要查找24，则桶索引为hash(24)%11 = 24%11 = 2。

由于哈希值是无符号整数，其范围比数组长度大得多，因此两个不同的key可能对应同一个桶（例如上图中的24和35），这就是散列冲突(hash collision)。一种解决方法是溢出表法，即将同一个桶中的元素组织成链表。上面的示例采用的就是溢出表法。

散列表的主要优点是查找的平均时间复杂度接近于 $O(1)$ （即常数，与元素个数无关），但最差情况下为 $O(N)$ （即所有key集中在同一个桶，此时散列表退化为链表）。

STL unordered_map就是使用散列表实现的映射。使用STL容器的经验法则是：

• 除非有好的理由，否则使用vector。
• 如果需要基于key查询value，并且key有序，则使用map。
• 如果需要在大的映射中进行大量查找，并且不需要按顺序遍历，则使用unordered_map。

注：核心STL容器各种操作的时间复杂度对比如下

操作/容器	vector	list	map	unordered_map
[]/at()	$O(1)$	-	$O(\log n)$	平均 $O(1)$ ，最差 $O(n)$
push_back()	$O(1)$	$O(1)$	-	-
insert()	$O(n)$	$O(1)$	$O(\log n)$	平均 $O(1)$ ，最差 $O(n)$
erase()	$O(n)$	$O(1)$	$O(\log n)$	平均 $O(1)$ ，最差 $O(n)$
find()	$O(n)$	$O(n)$	$O(\log n)$	平均 $O(1)$ ，最差 $O(n)$

注：

• list插入和删除时间复杂度为 $O(1)$ 的前提是已经有插入/删除位置的迭代器，而这个迭代器通常是通过遍历或者搜索算法获得的。
• 表格中map的插入和删除操作是指给定一个key，另外也有给定插入/删除位置迭代器的版本，其时间复杂度为 $O(1)$ 。

21.6.5 set

集合(set)即只有key、没有value的映射。set节点如下图所示：

用set表示21.6.2节水果的示例：

集合可用于记住见过的值、去重等用途。

和map一样，set的元素是有序的（默认使用<比较）。如果使用自定义类型作为set的元素类型，则需要为自定义类型定义operator<，或通过模板参数指定比较操作（函数对象）：

struct Fruit {
    string name;
    int count;
    double unit_price;
    Date last_sale_date;
    // ...
};

struct Fruit_order {
    bool operator()(const Fruit& a, const Fruit& b) const {
        return a.name < b.name;
    }
};

set<Fruit, Fruit_order> inventory;  // use Fruit_order(x,y) to compare Fruits (by name)

由于map和set不是线性数据结构，因此不支持[]和push_back()，增删元素必须使用insert()和erase()。例如：

inventory.insert(Fruit("quince", 5));
inventory.insert(Fruit("apple", 200, 0.37));

由于set没有map的(key, value)对，因此可以直接对key迭代：

for (auto p = inventory.begin(); p != inventory.end(); ++p)
    cout << *p << '\n';

当然也可以使用基于范围的for循环：

for (const auto& x : inventory)
    cout << x << '\n';

21.7 拷贝操作

STL提供了三个版本的拷贝操作：

拷贝算法	功能
copy(b, e, b2)	将[b, e)拷贝到[b2, b2+(e-b))
unique_copy(b, e, b2)	将[b, e)拷贝到[b2, b2+(e-b))，不拷贝相邻的重复元素
copy_if(b, e, b2, p)	将[b, e)拷贝到[b2, b2+(e-b))，但只拷贝满足谓词p的元素

这些算法定义在<algorithm>中。

21.7.1 拷贝

基本的拷贝算法定义如下：

template<class InputIt, class OutputIt>
OutputIt copy(InputIt first, InputIt last, OutputIt result) {
    for (; first != last; ++first, ++result)
        *result = *first;
    return result;
}

例如：

// copy the elements of a list of ints into a vector of doubles
void f(vector<double>& vd, list<int>& li) {
    if (vd.size() < li.size()) error("target container too small");
    copy(li.begin(), li.end(), vd.begin());
    // ...
}

注意，输入序列的类型和元素类型可以与输出序列不同，这正是STL算法的通用性。使用copy()时，我们必须检查输出序列是否有足够的空间来保存元素。

注：copy()只是拷贝元素，并不插入新元素。如果希望在向量结尾插入新元素，可以使用以下几种方法：

• 直接使用迭代器初始化：vector<double> vd(li.begin(), li,end());
• 先使用resize()预留空间：vd.resize(li.size()); copy(li.begin(), li.end(), vd.begin());
• 使用insert()：vd.insert(vd.end(), li.begin(), li.end());
• 使用back_inserter：copy(li.begin(), li.end(), back_inserter(v));

21.7.2 流迭代器

和容器迭代器不同，流迭代器的操作对象是I/O流而不是容器。

ostream_iterator向ostream写数据（使用<<运算符）。例如：

ostream_iterator<string> oo(cout);  // assigning to *oo is to write to cout

*oo = "Hello, ";    // meaning cout << "Hello, "
++oo;               // “get ready for next output operation”
*oo = "World!\n";   // meaning cout << "World!\n"

类似地，istream_iterator从istream读数据（使用>>运算符）。例如：

istream_iterator<string> ii(cin);   // reading *ii is to read a string from cin

string s1 = *ii;    // meaning cin>>s1
++ii;               // “get ready for the next input operation”
string s2 = *ii;    // meaning cin>>s2

istream_iterator和ostream_iterator定义在<iterator>中，迭代器类别分别是输入迭代器和输出迭代器（见20.10.1节）。

注：实际上，istream_iterator的++运算符调用istream的>>运算符，*返回读取的值；ostream_iterator的=运算符调用ostream的<<运算符，而*和++什么都不做。简化的定义如下：

template<class T>
class istream_iterator {
public:
    istream_iterator() :is(nullptr) {}
    istream_iterator(istream& is) :is(&is) { read(); }

    const T& operator*() const { return val; }
    istream_iterator& operator++() { read(); return *this; }
    bool operator==(const istream_iterator& rhs) const { return is == rhs.is; }

private:
    void read() {
        if (!(*is >> val))
            is = nullptr;
    }

    istream* is;
    T val;
};

template<class T>
class ostream_iterator {
public:
    ostream_iterator(ostream& os, const char* delim = nullptr) :os(&os), delim(delim) {}

    ostream_iterator& operator=(const T& val) {
        *os << val;
        if (delim)
            *os << delim;
        return *this;
    }

    ostream_iterator& operator*() { return *this; }
    ostream_iterator& operator++() { return *this; }

private:
    ostream* os;
    const char* delim;
};

使用流迭代器，就可以将copy()等STL算法用于I/O。例如，我们可以实现一个“简陋的”字典（从一个文件中读取单词，排序并去重，然后输出到另一个文件）：

简单字典v2

迭代器eos是istream_iterator对“输入结束”的表示。当istream到达输入结尾或读取失败时，它的istream_iterator将会等于其默认值。

注：从上面的简化定义中可以看出，istream_iterator的成员is是其绑定的istream的指针，默认构造函数将其置为nullptr。当++读取失败时，也会将该指针置为nullptr，从而与默认迭代器相等。

注意，我们使用一对迭代器来初始化向量b。STL容器可以使用一对迭代器first和last来初始化，表示使用[first, last)中的元素构造容器。这里我们使用了ii和eos，即从输入读取，从而不需要显式使用>>和push_back()。

我们强烈不建议猜测最大输入数量，否则可能导致缓冲区溢出（越界访问）：

vector<string> b(max_size);  // don't guess about the amount of input!
copy(ii, eos, b.begin());

如果输入

the man bit the dog

程序将会输出

bit
dog
man
the

ostream_iterator构造函数允许你（可选地）指定在输出每个值之后打印的分隔字符串：

ostream_iterator<string> oo(os, "\n");  // make output iterator for stream

21.7.3 使用set保持顺序

对单词排序更简单的方法是使用set：

set<string> b(istream_iterator<string>(is), istream_iterator<string>());
copy(b.begin(), b.end(), ostream_iterator<string>(os, " ");  // copy buffer to output

当我们向set中插入元素时，重复的元素将被忽略。另外，set的元素是有序的，因此不需要排序。

使用正确的工具，大多数任务都很容易完成。

21.7.4 copy_if

第三种拷贝算法copy_if()只拷贝满足条件的元素：

template<class InputIt, class OutputIt, class Pred>
OutputIt copy(InputIt first, InputIt last, OutputIt result, Pred p) {
    for (; first != last; ++first)
        if (p(*first))
            *result++ = *first;
    return result;
}

例如，拷贝一个序列中所有大于6的元素：

// copy all elements with a value larger than 6
void f(const vector<int>& v) {
    vector<int> v2(v.size());
    copy_if(v.begin(), v.end(), v2.begin(), Larger_than(6));
    // ...
}

21.8 排序和搜索

通常，我们希望数据是有序的。我们可以通过使用有序数据结构（例如map和set）或者排序来实现。在STL中，最常用的排序操作是sort()，我们已经多次使用过。默认情况下，sort()使用<比较元素，但是也可以自定义规则：

template<class RandomIt>
void sort(RandomIt first, RandomIt last);

template<class RandomIt, class Compare>
void sort(RandomIt first, RandomIt last, Compare comp);

注意：模板参数RandomIt必须是随机访问迭代器，因此不能使用sort()对list排序，而应该使用list::sort()。

例如，排序字符串向量（不区分大小写）：

排序字符串（不区分大小写）

注：函数对象No_case实现不区分大小写比较两个字符串的方法（类似于Java中的String.compareToIgnoreCase()），作为sort()算法的自定义比较规则。另一种实现方法是使用tolower() + lexicographical_compare()，如compare_string_ignore_case()所示。

使用std::greater可以实现倒序排序：

std::sort(v.begin(), v.end(), greater<int>());

如果一个序列已经排好序，就没有必要使用find()从头开始搜索，可以使用二分搜索(binary search)。

注：另见《C程序设计语言》笔记 第3章 控制流 3.3节。

二分搜索的基本思想如下：假设要查找值x，查看中间元素

• 如果中间元素等于x，则已经找到；
• 如果中间元素小于x，则在右半部分进行二分搜索；
• 如果中间元素大于x，则在左半部分进行二分搜索；
• 如果已经达到最后一个元素，则不存在等于x的元素。

二分搜索的伪代码如下：

binary_search(a, x) {
    left = 0
    right = a.length
    while (left < right) {
        mid = (left + right) / 2
        if (a[mid] < x)
            left = mid + 1
        else
            right = mid
    }
    return a[left] == x
}

对于长度为n的有序序列，线性搜索find()的时间复杂度为 $O(n)$ ，二分搜索的时间复杂度为 $O(\log n)$ 。

标准库的二分搜索算法是binary_search()：

template<class ForwardIt, class T>
bool binary_search(ForwardIt first, ForwardIt last, const T& value);

template<class ForwardIt, class T, class Compare>
bool binary_search(ForwardIt first, ForwardIt last, const T& value, Compare comp);

注意：二分搜索算法要求输入序列是有序的，否则可能发生意想不到的事情（例如无限循环）。

注：对于随机访问容器（例如vector），binary_search()的时间复杂度是 $O(\log n)$ ，而对于不可随机访问的容器（例如list），时间复杂度是 $O(n\log n)$ 。

binary_search()只返回一个值在序列中是否存在。如果需要元素位置，可以使用lower_bound()、upper_bound()或equal_range()。

二分搜索算法	功能
binary_search(b, e, v)	判断v在有序序列[b, e)中是否存在
lower_bound(b, e, v)	返回有序序列[b, e)中第一个不小于v的元素的迭代器
upper_bound(b, e, v)	返回有序序列[b, e)中第一个大于v的元素的迭代器
equal_range(b, e, v)	返回有序序列[b, e)中等于v的范围的起止迭代器

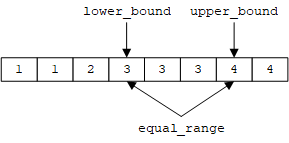
例如，对于序列[1, 1, 2, 3, 3, 3, 4, 4]，v = 3

对于不存在的元素，这三个算法返回的迭代器相同，即按顺序插入该元素的位置。

21.9 容器算法

std_lib_facilities.h中提供了一些将整个容器作为参数的算法。例如：

template<class C>
void sort(C& c) {
    std::sort(c.begin(), c.end());
}

简单练习

• 21-1
• 21-2
• 21-3

习题

• 21-3~21-4
• 21-6
• 21-7
• 21-8
• 21-9~21-10
  • Order类
  • 主程序
• 21-11~21-12
  • Order_list_window
  • Order_list_table
  • Order_edit_window
  • Purchase_list_table
  • 主程序
• 21-13~21-15
  • Word_query
  • Word_query_window
  • 主程序