《C++程序设计原理与实践》笔记 第24章 数值计算

本章将介绍用于数值计算的一些基本语言特性和标准库功能。

24.1 引言

本章的目的是介绍一些用于处理简单数值计算(numerics)问题的语言技术细节：

• 与内置类型相关的问题，例如精度和溢出
• 内置多维数组和Matrix库
• 随机数
• 标准库数学函数
• 复数

24.2 大小、精度和溢出

当我们使用内置类型时，数字被存储在固定大小的内存中。也就是说，整数类型（int、long等）只是数学上整数概念的近似，浮点类型（float、double等）只是数学上实数概念的近似。这意味着从数学的角度，某些计算是不精确甚至错误的。例如：

float x = 1.0 / 333;
float sum = 0;
for (int i = 0; i < 333; ++i) sum += x;
cout << setprecision(15) << sum << "\n";

程序输出 “0.999999463558197” 而不是期望的 “1” ——这就是舍入误差(rounding error)的影响。一个float只有4字节（32位），而实数有无限多个，因此计算机无法精确表示实数（这类似于使用十进制的6位小数无法精确表示1/3）。每当我们进行大量浮点运算时，就会产生舍入误差，唯一的问题是误差对结果的影响是否严重。

【试一试】将例子中的333改为10，结果仍然有误差：1.00000011920929。

注：

• double类型的精度比float更高。例如，0.1f + 0.2f输出 “0.300000011920929” ，而0.1 + 0.2输出 “0.3” 。
• 当浮点数的绝对值非常大时，舍入误差的绝对值也会非常大，但相对误差很小。例如，绝对误差6e23f + 2e21f - 6.02e23f约为 -3.60288e+16，而相对误差(6e23f + 2e21f) / 6.02e23f - 1约为 -5.96046e-08。因此，不能用==判断两个浮点数是否相等，而应该判断误差的绝对值是否小于一定的阈值。对于小的浮点数应使用绝对误差(fabs(x - y) < 1e-6)，对于大的浮点数应使用相对误差(fabs(x / y - 1) < 1e-6)。另见《C程序设计语言》笔记 第2章 “浮点数常量 ”一节。
• 其他语言也存在类似的问题。例如，在Python中：

>>> 0.1 + 0.2
0.30000000000000004

浮点数的问题在于损失精度（即丢失最低有效位），而整数的问题在于溢出(overflow)（即丢失最高有效位）。例如：

short int y = 40000;
int i = 1000000;
cout << y << " " << i*i << "\n";

输出结果为 “-25536 -727379968” 。

这是因为计算机内存中的整数类型是固定大小的，n个二进制位只能表示2ⁿ个不同的整数。n位有符号整数的范围是-2^n-1~2^n-1-1，无符号整数的范围是0~2ⁿ-1。例如，2字节（16位）short的范围是-32768~32767，不能表示40000；4字节（32位）int的范围是-2147483648~2147483647，不能表示1000000000000。

注：C++标准规定，无符号整数运算始终是模2ⁿ（例如4294967295u + 1u == 0u），而有符号整数溢出是未定义行为，见Arithmetic operators - Overflows。这意味着不同平台、不同编译器、不同优化模式可能会有不同的结果，例如Issue #13。

C++内置整数类型的具体大小取决于硬件和编译器。sizeof(x)是变量或类型x的大小（单位是字节），根据C++标准定义sizeof(char) == 1。

注：

• 详见17.3.1节、《C程序设计语言》笔记 第2章 2.2节和Fundamental types “Integer types” 一节。
• 标准库头文件<cstdint>定义了一组固定宽度整数类型（别名），例如int32_t、int64_t等。

可以将整数赋值给浮点数，但可能会丢失精度。例如：

cout << "sizes: " << sizeof(int) << ' ' << sizeof(float) << '\n';
int x = 2100000009;     // large int
float f = x;
cout << x << ' ' << f << '\n';
cout << setprecision(15) << x << ' ' << f << '\n';

输出结果为

sizes: 4 4           
2100000009 2.1e+09   
2100000009 2100000000

虽然float和int都是4字节，但float在内存中表示为一个尾数(mantissa)和一个指数(exponent)，即尾数*10^指数。而尾数的精度有限，因此float无法精确表示整数2100000009。

另一方面，将浮点数赋值给整数会导致截断(truncation)，即小数部分被丢弃。例如：

float f = 2.8;
int x = f;
cout << x << ' ' << f << '\n';

将输出 “2 2.8” 。C++中float到int的转换是截断而非舍入。

当进行计算时，你必须清楚可能的溢出和截断。C++不会捕获这些问题。考虑下面的程序：

溢出和截断

对于这类问题，实验是最好的方法。

如果可能，应该使用尽可能少的类型，这有助于减少混乱。我们倾向于只使用int、double和complex（见24.9节）来计算，只使用char表示字符，只使用bool进行逻辑运算。

24.2.1 数值限制

标准库头文件<climits>、<cfloat>和<limits>指定了内置类型的最小值和最大值。例如：

数值限制

24.3 数组

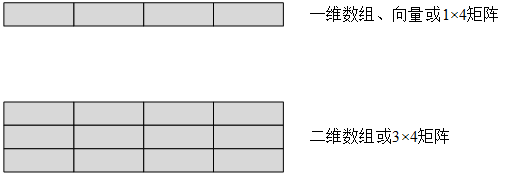
数组(array)是一个元素的序列，可以通过索引（位置/下标）访问元素，通常也称为向量(vector)。多维数组(multidimensional array)即元素本身也是数组的数组，通常也称为矩阵(matrix)。

内置数组、std::vector和std::array都是一维的。二维数组由行和列组成：

24.4 C风格多维数组

C++内置数组可以创建多维数组。例如：

int ai[4];          // 1-dimensional array
double ad[3][4];    // 2-dimensional array
char ac[3][4][5];   // 3-dimensional array
ai[1] = 7;
ad[2][3] = 7.2;
ac[2][3][4] = 'c';

其中，ad是大小为3×4的二维数组，每个元素ad[i]是长度为4的一维数组；ac是大小为3×4×5的三维数组，每个元素ac[i]是大小为4×5的二维数组。

多维数组继承了一维数组的优点和缺点：

• 优点：直接映射到硬件，底层操作效率高，语言直接支持。
• 缺点：固定大小，没有越界检查，没有数组操作（拷贝和赋值），不能干净地传递参数（只能转换为首元素的指针）。

多维数组最大的问题在于不能干净地传递参数，而必须退化为指针，并显式计算元素位置。例如：

void f1(int a[3][5]);                   // useful for [3][5] matrices only
void f2(int a[][5], int dim1);          // 1st dimension can be a variable
void f3(int a[5][], int dim2);          // error: 2nd dimension cannot be a variable
void f4(int a[][], int dim1, int dim2); // error (and wouldn't work anyway)
void f5(int* m, int dim1, int dim2) {   // odd, but works
    for (int i = 0; i < dim1; ++i)
        for (int j = 0; j < dim2; ++j) m[i * dim2 + j] = 0;
}

注：

• f2()的参数int a[][5]叫做行指针，可以通过a[i][j]的形式访问元素，但第二维大小必须是固定的。f5()的参数int* m叫做列指针，编译器不知道m是一个二维数组，必须通过m[i*dim2+j]显式计算元素在内存中的位置。详见二维数组的行指针和列指针。
• 另见《C程序设计语言》笔记 第5章 5.9节。

这太复杂、太原始、太容易出错了。因此我们不再介绍多维数组，而是重点关注Matrix库，它解决了上述问题。

24.5 Matrix库

我们希望从一个用于数值计算的矩阵库获得什么基本功能？

• 代码应该看起来和数学教科书上矩阵的表示方式相似
• 编译时和运行时检查（维数、每一维的元素个数）
• 矩阵是真正的对象（可以作为参数传递）
• 支持常见的矩阵运算
  • 下标()
  • 切片[]
  • 赋值=
  • 标量运算(+=、-=、*=、%=等)
  • 混合向量运算（例如res[i] = a[i] * c + b[2]）
  • 点积（res等于a[i] * b[i]的和）
• 可以将传统数组/向量的概念转换为代码
• 可以按需扩展

Matrix库实现了上述功能（也只实现了这些）。Matrix库不是C++标准库的一部分，而是作者提供的。可以从作者网站上下载code.tar，解压后在code/Chapter24目录下找到Matrix.h和MatrixIO.h，或者从GitHub仓库下载。整个库定义在命名空间Numeric_lib中。

24.5.1 维度和访问

考虑一个简单的例子：

矩阵示例

定义Matrix对象时，需要指定元素类型和维数，二者都是模板参数，维数默认为1。例如，ad1是double类型的一维矩阵Matrix<double, 1>。构造函数参数指定每一位的大小。例如，ad2是二维矩阵，大小为n1×n2。为了获取元素，使用()指定下标，n维矩阵需要n个下标。例如ad1(7)、ad2(3, 4)、ad3(3, 4, 5)等。矩阵下标是从0开始的。

注意，Matrix支持()和[]两种下标操作。如果a是n维矩阵，a(i1, i2, ..., in)返回一个元素，下标个数必须等于维数；而a[i]返回一个n-1维矩阵。对于一维矩阵，二者等价。

赋值操作=要求元素类型、维数以及各维大小完全相同。

下面是一些错误的用法：

void f(int n1, int n2, int n3) {
    Matrix<int, 0> ai0;     // error: no 0D matrices

    Matrix<double, 1> ad1(5);
    Matrix<int, 1> ai(5);
    Matrix<double, 1> ad11(7);

    ad1(7) = 0;     // Matrix_error exception (7 is out of range)
    ad1 = ai;       // error: different element types
    ad1 = ad11;     // Matrix_error exception (different dimensions)

    Matrix<double, 2> ad2(n1);  // error: length of 2nd dimension missing
    ad2(3) = 7.5;               // error: wrong number of subscripts
    ad2(1, 2, 3) = 7.5;         // error: wrong number of subscripts

    Matrix<double, 3> ad3(n1, n2, n3);
    Matrix<double, 3> ad33(n1, n2, n3);
    ad3 = ad33;     // OK: same element type, same dimensions
}

其中错误的原因：

• Matrix<int, 0> ai0：编译时错误，模板Matrix<T,D>的构造函数声明为private，禁止实例化。只有模板特化Matrix<T,1>、Matrix<T,2>和Matrix<T,3>可以实例化。
• ad1(7) = 0：运行时错误，Matrix<T,1>::operator()范围检查失败，抛出Matrix_error异常。
• ad1 = ai：编译时错误，Matrix<T,1>::operator=的参数矩阵必须和被赋值矩阵是相同类型。
• ad1 = ad11：运行时错误，Matrix<T,1>::operator=的参数矩阵大小必须和被赋值矩阵相同，抛出Matrix_error异常。
• Matrix<double, 2> ad2(n1)：编译时错误，Matrix<T,2>的构造函数接受两个参数。
• ad2(3) = 7.5和ad2(1, 2, 3) = 7.5：编译时错误，Matrix<T,2>::operator()接受两个参数。

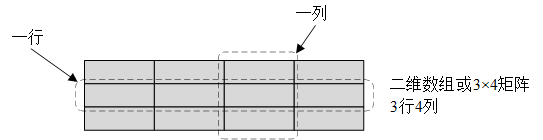
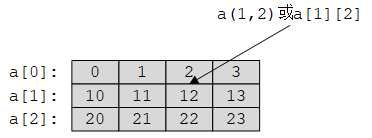
二维矩阵的第一维是行，第二维是列，因此使用a(row, column)来索引。也可以使用a[row][column]，因为a[row]是一个一维矩阵，即第row行。如下图所示：

二维矩阵在内存中以“行主次序”(“row-first” order)存放：

Matrix知道自己的大小，因此可以很容易地访问元素和作为参数传递：

二维矩阵

dim1()是第一维的大小，dim2()是第二维的大小，以此类推。

元素类型和维数是Matrix类型的一部分，因此无法编写一个接受任意Matrix参数的函数（除非使用模板）：

void init(Matrix& a);   // error: element type and number of dimensions missing

注意，Matrix库不支持矩阵运算（例如矩阵加法、矩阵乘法），但可以在Matrix库之上设计这些算法（见习题12）。

24.5.2 一维矩阵

最简单的一维Matrix可以进行什么操作？

声明时可以省略维数：

Matrix<int, 1> a1(8);   // a1 is a 1D Matrix of ints
Matrix<int> a(8);       // means Matrix<int,1> a(8);

可以获取矩阵大小（元素个数）和第一维的大小。对于一维矩阵，二者相同。

a.size();   // number of elements in Matrix
a.dim1();   // number of elements in 1st dimension

可以获取内存中的元素，即指向第一个元素的指针：

int* p = a.data();  // extract data as a pointer to an array

可以通过下标访问元素：

a(i);   // ith element (Fortran style), but range checked
a[i];   // ith element (C style), range checked

可以使用slice()引用矩阵的一部分（子矩阵或“切片”(slice)）：

a.slice(i);     // the elements from a[i] to the last
a.slice(i, n);  // the n elements from a[i] to a[i+n-1]

即a.slice(i, n)表示区间[i, i+n)，a.slice(i)表示区间[i, a.dim1())。

下标和切片既可以用在赋值号左侧，也可以在右侧。例如：

a.slice(4, 4) = a.slice(0, 4);  // assign first half of a to second half

如果a开始为{ 1 2 3 4 5 6 7 8 }，则得到{ 1 2 3 4 1 2 3 4 }。

如果a.slice(i, n)中的i和n超过a的范围，则结果只取有效范围。例如，a的大小为8，则a.slice(5, 10)等价于a.slice(5, 3)，a.slice(4, 0)为空。

拷贝操作会拷贝所有元素：

Matrix<int> a2 = a; // copy initialization
a = a2;             // copy assignment

可以对Matrix的每个元素进行算术运算：

a *= 7;     // scaling: a[i]*=7 for each i (also +=, -=, /=, etc.)
a = 7;      // a[i]=7 for each i

也可以对每个元素应用一个函数：

a.apply(f);     // a[i]=f(a[i]) for each element a[i]
a.apply(f, 7);  // a[i]=f(a[i],7) for each element a[i]

例如：

void scale_in_place(double& d, double s) { d *= s; }
b.apply(scale_in_place, 7); // b[i] *= 7 for each i

赋值运算符和apply()修改了Matrix的元素。如果希望创建一个新的Matrix，可以使用非成员函数版本的apply()：

b = apply(abs, a);  // make a new Matrix with b(i)==abs(a(i))

相应地，也提供了两个参数的版本：

b = apply(f, a, x); // b[i]=f(a[i],x) for each i

例如：

double scale(double d, double s) { return d * s; }
b = apply(scale, a, 7);     // b[i] = a[i]*7 for each i

注意：scale_in_place()会修改参数，因此第一个参数是引用，没有返回值；scale()不修改参数，而是返回结果。

另外还提供了传统数值计算库中的一些常用函数：

Matrix<int> a3 = scale_and_add(a, 8, a2);   // fused multiply and add: a3[i]=a[i]*8+a2[i]
int r = dot_product(a3, a);                 // dot product: r=sum(a3[i]*a[i])

其中，scale_and_add()称为乘加混合运算(fused multiply-add, FMA)，定义为result(i)=arg1(i)*arg2+arg3(i)。dot_product()是点积（内积），定义为result=sum(arg1(i)*arg2(i))，如21.5.3节所述。

注：标准库头文件<valarray>提供了支持数值运算的一维数组std::valarray。另外，习题19-1也实现过简单的向量加法。

总之，Matrix的操作（例如拷贝、赋值、运算等）是对所有元素进行操作，使我们不必编写循环代码。

除了指定大小，Matrix构造函数还支持从内置数组拷贝数据：

void some_function(double* p, int n) {
    double val[] = {1.2, 2.3, 3.4, 4.5};
    Matrix<double> data(p, n);
    Matrix<double> constants(val);
    // ...
}

24.5.3 二维矩阵

Matrix库的总体思想是：不同维数的矩阵除了维数之外是非常相似的。因此一维矩阵的大部分操作都适用于二维矩阵：

Matrix<int, 2> a(3, 4);

int s = a.size();   // number of elements
int d1 = a.dim1();  // number of elements in a row
int d2 = a.dim2();  // number of elements in a column
int* p = a.data();  // extract data as a pointer to a C-style array

二维矩阵支持下标：

a(i, j);    // (i,j)th element (Fortran style), but range checked
a[i];   // ith row (C style), range checked
a[i][j];    // (i,j)th element (C style)

对于二维矩阵，下标[i]获得第i行，即一个一维矩阵。这意味着可以提取行并传递给需要一维矩阵的函数。

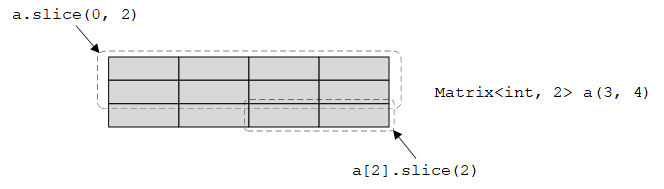
二维矩阵也支持切片：

a.slice(i);     // the rows from the a[i] to the last
a.slice(i, n);  // the rows from the a[i] to the a[i+n-1]

注意，二维矩阵的切片仍然是二维矩阵。

二维矩阵的标量操作和一维矩阵相同：

Matrix<int, 2> a2 = a;  // copy initialization
a = a2;                 // copy assignment
a *= 7;                 // scaling (and +=, -=, /=, etc.)
a.apply(f);             // a(i,j)=f(a(i,j)) for each element a(i,j)
a.apply(f, 7);          // a(i,j)=f(a(i,j),7) for each element a(i,j)
b = apply(f, a);        // make a new Matrix with b(i,j)==f(a(i,j))
b = apply(f, a, 7);     // make a new Matrix with b(i,j)==f(a(i,j),7)

交换行通常是有用的：

a.swap_rows(1, 2);  // swap rows a[1] <-> a[2]

并没有swap_columns()，如果需要可以自己实现（习题11）。原因在于元素是按行主次序存储的，行和列并不是完全对称的概念。这也体现在[i]获取行，而没有获取列的运算符。

注：作者提供的代码中Matrix<T,1>::swap_rows()实现有错误，应改为：

void swap_rows(Index i, Index j) {
    std::swap((*this)(i), (*this)(j));
}

在现实世界中，有很多事物都是二维的，因此显然可以用二维矩阵来描述。例如，国际象棋的棋盘可以用8×8的二维矩阵来表示：

下面的代码初始化棋盘：

enum Piece { none, pawn, knight, queen, king, bishop, rook };
Matrix<Piece, 2> board(8, 8);   // a chessboard

const int white_start_row = 0;
const int black_start_row = 7;

Matrix<Piece> start_row = {rook, knight, bishop, queen, king, bishop, knight, rook};
Matrix<Piece> clear_row(8);     // 8 elements of the default value

board[white_start_row] = start_row;                 // reset white pieces
for (int i = 1; i < 7; ++i) board[i] = clear_row;   // clear middle of the board
board[black_start_row] = start_row;                 // reset black pieces

24.5.4 矩阵I/O

Matrix库为一维和二维矩阵提供的非常简单的I/O功能：

Matrix<double> a(4);
cin >> a;
cout << a;

一维矩阵的I/O格式为：元素之间用空白符分隔，两边用花括号括起来。例如：

{ 1.2 3.4 5.6 7.8 }

二维矩阵的I/O格式为花括号括起来的一维矩阵的序列。例如：

Matrix<int,2> m(2, 2);
cin >> m;
cout << m;

{
{ 1 2 }
{ 3 4 }
}

Matrix的<<和>>运算符定义在头文件MatrixIO.h中。

24.5.5 三维矩阵

三维矩阵与二维矩阵相似，除了多一个维度。

Matrix<int, 3> a(10, 20, 30);

a.size();           // number of elements
a.dim1();           // number of elements in dimension 1
a.dim2();           // number of elements in dimension 2
a.dim3();           // number of elements in dimension 3
int* p = a.data();  // extract data as a pointer to a C-style array

a(i, j, k);         // (i,j,k)th element (Fortran style), but range checked
a[i];               // ith row (C style), range checked
a[i][j][k];         // (i,j,k)th element (C style)
a.slice(i);         // the rows from the ith to the last
a.slice(i,j);       // the rows from the ith to the jth

Matrix<int, 3> a2 = a;  // copy initialization
a = a2;                 // copy assignment
a *= 7;                 // scaling (and +=, -=, /=, etc.)
a.apply(f);             // a(i,j,k)=f(a(i,j,k)) for each element a(i,j,k)
a.apply(f, 7);          // a(i,j,k)=f(a(i,j,k),7) for each element a(i,j,k)
b = apply(f, a);        // make a new Matrix with b(i,j,k)==f(a(i,j,k))
b = apply(f, a, 7);     // make a new Matrix with b(i,j,k)==f(a(i,j,k),7)
a.swap_rows(7, 9);      // swap rows a[7] <-> a[9]

如果a是三维矩阵，则a[i]是二维矩阵，a[i][j]是一维矩阵，a[i][j][k]和a(i, j, k)是元素。

24.6 示例：解线性方程组

求解线性方程组是矩阵的一个非常重要的应用。其目标是求解下面这种形式的线性方程组：

\[\begin{cases} a_{11}x_1 + \cdots + a_{1n}x_n = b_1 \newline \cdots \newline a_{n1}x_1 + \cdots + a_{nn}x_n = b_n \end{cases}\]

其中， $x_j$ 表示n个未知数， $a_{ij}$ 和 $b_i$ 是给定的常量。目标是找到同时满足n个方程的未知数。

方程组可以表示为矩阵形式：

\[\mathbf{Ax} = \mathbf{b}\]

其中

\[\mathbf{A} = \begin{bmatrix} a_{11} & \cdots & a_{1n} \newline \vdots & \ddots & \vdots \newline a_{n1} & \cdots & a_{nn} \end{bmatrix}, \mathbf{x} = \begin{bmatrix} x_1 \newline \vdots \newline x_n \end{bmatrix}, \mathbf{b} = \begin{bmatrix} b_1 \newline \vdots \newline b_n \end{bmatrix}\]

该方程组可能有0个、1个或无穷多个解，这取决于系数矩阵A和向量b。

求解线性方程组的方法有很多。本节使用一种经典的方法——高斯消元法(Gaussian elimination)。首先，对A和b进行变换，使A变成上三角矩阵，即对角线下方的元素均为0：

\[\begin{bmatrix} a_{11} & \cdots & a_{1n} \newline 0 & \ddots & \vdots \newline 0 & 0 & a_{nn} \end{bmatrix} \begin{bmatrix} x_1 \newline \vdots \newline x_n \end{bmatrix} = \begin{bmatrix} b_1 \newline \vdots \newline b_n \end{bmatrix}\]

如果变换可以使得所有对角线上的元素非零，则方程组有唯一解，可以通过“代回”(back substitution)得到：首先由最后一个方程得到 $x_n = b_n / a_{nn}$ ，之后代入第n-1个方程得到 $x_{n-1}$ ，以此类推，直至求解出 $x_1$ 。

24.6.1 经典高斯消元法

下面用C++代码来表达上述算法。首先，为了方便表示，引入两个别名：

using Matrix = Numeric_lib::Matrix<double, 2>;
using Vector = Numeric_lib::Matrix<double, 1>;

• 高斯消元法
• 主程序

函数classical_gaussian_elimination()将问题分解为两步：

• 消元：classical_elimination()
• 代回：back_substitution()

解决方案完全来自于教科书。“主元”(pivot)表示当前行位于对角线上的元素，如果为0则抛出异常。

下面以三元一次方程组为例对消元过程进行解释：

\[\begin{bmatrix} a_{11} & a_{12} & a_{13} \newline a_{21} & a_{22} & a_{23} \newline a_{31} & a_{32} & a_{33} \end{bmatrix} \begin{bmatrix} x_1 \newline x_2 \newline x_3 \end{bmatrix} = \begin{bmatrix} b_1 \newline b_2 \newline b_3 \end{bmatrix}\]

第一步：将第2行和第3行分别减去第1行的 $\frac{a_{21}}{a_{11}}$ 和 $\frac{a_{31}}{a_{11}}$ 倍，消去所有的 $a_{i1} (i \ge 2)$ （对应代码中外层循环的j = 0，公式中下标从1开始），得到：

\[\begin{bmatrix} a_{11} & a_{12} & a_{13} \newline 0 & a_{22} - \frac{a_{21}}{a_{11}}a_{12} & a_{23} - \frac{a_{21}}{a_{11}}a_{13} \newline 0 & a_{32} - \frac{a_{31}}{a_{11}}a_{12} & a_{33} - \frac{a_{31}}{a_{11}}a_{13} \end{bmatrix} \begin{bmatrix} x_1 \newline x_2 \newline x_3 \end{bmatrix} = \begin{bmatrix} b_1 \newline b_2 - \frac{a_{21}}{a_{11}}b_1 \newline b_3 - \frac{a_{31}}{a_{11}}b_2 \end{bmatrix}\]

第二步：设上一步更新后的系数为 $a_{ij}’$ 和 $b_i’$ 。将第3行减去第2行的 $\frac{a_{32}’}{a_{22}’}$ 倍，消去所有的 $a_{i2} (i \ge 3)$ （对应代码中外层循环的j = 1），得到：

\[\begin{bmatrix} a_{11} & a_{12} & a_{13} \newline 0 & a_{22}' & a_{23}' \newline 0 & 0 & a_{33}' - \frac{a_{32}'}{a_{22}'}a_{23}' \end{bmatrix} \begin{bmatrix} x_1 \newline x_2 \newline x_3 \end{bmatrix} = \begin{bmatrix} b_1 \newline b_2' \newline b_3' - \frac{a_{32}'}{a_{22}'}b_2' \end{bmatrix}\]

从而将矩阵A转换为上三角矩阵。之后通过代回法依次解出x3、x2和x1即可。

24.6.2 选取主元

为了避免除以零的问题，我们可以对行排序，将0和较小的值从对角线上移开，从而得到一个更鲁棒的解决方案。“更鲁棒”(more robust)（即“更健壮”）是指对舍入误差更不敏感。

函数elim_with_partial_pivot()实现了这一方法。

24.6.3 测试

显然，我们必须测试代码。有一种简单的方法——随机生成：

解随机线性方程组

有三种情况会进入catch子句：

• 代码有bug（作为乐观主义者，我们认为没有）
• 输入使classical_elimination()遇到对角线元素为0（即方程组无解或不是唯一解）
• 舍入误差

为了验证解，我们打印出A*x，应该与b相等。考虑到舍入误差，我们并没有这样判断：

if (A*x != b) error("substitution failed");

因为浮点数只是实数的近似，一般来说应该避免使用==和!=比较浮点数（如24.2节所述）。

Matrix库并没有定义矩阵与向量的乘法运算，因此我们为测试程序定义：

Vector operator*(const Matrix& m, const Vector& u) {
    const Index n = m.dim1();
    Vector v(n);
    for (Index i = 0; i < n; ++i) v(i) = dot_product(m[i], u);
    return v;
}

24.7 随机数

随机数(random number)并不是单个数字，而是指服从某种分布的数字序列，无法很容易地预测下一个数字。随机数在测试、游戏、仿真等领域非常有用。

C++11引入的标准库头文件<random>提供了一些用于生成随机数的功能，以匹配各种数学分布。标准库随机数功能基于两个基本概念：

• 随机数引擎(random number engine)/生成器(generator)：生成随机整数的函数对象。
• 分布(distribution)：给定随机数引擎作为输入，根据特定数学公式生成随机数的函数对象。

假设g是一个随机数引擎，d是一个分布，则g()返回区间[g.min(), g.max()]内的伪随机整数，d(g)返回服从特定分布的随机数（返回类型取决于d）。

例如，考虑24.6.3节中的random_vector()。调用random_vector(n)会生成一个具有n个元素的Vector（即Matrix<1, double>），元素值为[0, n)之间的随机数：

Vector random_vector(Index n) {
    Vector v(n);
    random_device rd;
    default_random_engine gen(rd());            // generates integers
    uniform_real_distribution<> ureal(0, n);    // maps ints into doubles in [0:n)

    for (Index i = 0; i < n; ++i)
        v(i) = ureal(gen);
    return v;
}

默认引擎default_random_engine对于一般情况就足够了。对于更专业的用途，标准库提供了各种具有更好随机性和不同运行成本的引擎。例如minstd_rand、mt19937等。uniform_real_distribution是均匀分布，用于生成区间[a, b)内的随机数。

注：

• default_random_engine实际上是一个类型别名，具体类型由实现定义。
• 随机数引擎使用种子(seed)（一个整数）初始化。相同的种子生成相同的随机数序列，不同的种子生成不同的随机数序列。例如，如果gen为默认构造，则每次调用random_vector(3)都会返回相同的向量（对于gcc编译器是{0.394613, 1.37595, 0.656878}），从而导致方程组有无穷多个解。
• random_device也是一个随机数引擎，但不适合直接用于生成随机数，通常只用于生成种子。详见cppreference示例。
• C标准库<cstdlib>也提供了生成随机数的函数rand()。
• （没有一种语言的标准库随机数像C++这样难用）

标准库提供的离散型分布如下表所示，模板参数T（随机数类型）必须是整数类型（int、long、unsigned int等），默认为int。

类模板	分布名称	参数	分布列
uniform_int_distribution<T>	均匀分布	$a, b$	$P(X=k)=\frac{1}{b-a+1}\;(a \le k \le b)$
bernoulli_distribution	伯努利分布（0-1分布）	$p$	$P(X=k)=\begin{cases} p,\;k=1 \newline 1-p,\;k=0 \end{cases}$
binomial_distribution<T>	二项分布	$n, p$	$P(X=k)=C_n^kp^k(1-p)^{n-k}\;(0 \le k \le n)$
negative_binomial_distribution<T>	负二项分布	$r, p$	$P(X=k)=C_{k-1}^{r-1}(1-p)^{k-1}p^r\;(k \ge r)$
geometric_distribution<T>	几何分布	$p$	$P(X=k)=(1-p)^{k-1}p\;(k \ge 1)$
poisson_distribution<T>	泊松分布	$\lambda$	$P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda}\;(k \ge 0)$

连续型分布如下表所示，模板参数T（随机数类型）必须是浮点类型（float、double或long double），默认为double。

类模板	分布名称	参数	概率密度函数
uniform_real_distribution<T>	均匀分布	$a, b$	$f(x)=\frac{1}{b-a}\;(a \le x < b)$
normal_distribution<T>	正态分布	$\mu, \sigma$	$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
exponential_distribution<T>	指数分布	$\lambda$	$f(x)=\lambda e^{-\lambda x}\;(x>0)$
gamma_distribution<T>	伽马分布	$\alpha, \beta$	$f(x)=\frac{x^{\alpha-1}e^{-\frac{x}{\beta}}}{\beta^\alpha\Gamma(\alpha)}\;(x>0)$
chi_squared_distribution<T>	卡方分布	$n$	$f(x)=\frac{x^{\frac{n}{2}-1}e^{-\frac{x}{2}}}{2^\frac{n}{2}\Gamma(\frac{n}{2})}\;(x>0)$
student_t_distribution<T>	t分布	$n$	$f(x)=\frac{\Gamma(\frac{n+1}{2})}{\sqrt{n\pi}\Gamma(\frac{n}{2})}(1+\frac{x^2}{n})^{-\frac{n+1}{2}}$
fisher_f_distribution<T>	F分布	$m, n$	$f(x)=\frac{\Gamma(\frac{m+n}{2})}{\Gamma(\frac{m}{2})\Gamma(\frac{n}{2})}(\frac{m}{n})^\frac{m}{2}x^{\frac{m}{2}-1}(1+\frac{m}{n}x)^{-\frac{m+n}{2}}\;(x>0)$

完整列表见<random>。

利用标准库的随机数功能，可以定义一个生成区间[a, b]内的随机整数的辅助函数：

int randint(int min, int max) {
    static default_random_engine ran;
    return uniform_int_distribution<>(min, max)(ran);
}

下面生成一个均匀分布：

auto gen = bind(normal_distribution<double>(15, 4.0), default_random_engine());

标准库函数bind()定义在<functional>中，返回一个函数对象，被调用时用第二个参数来调用第一个参数。在这里，gen()返回服从正态分布 $N(15, 4^2)$ 的随机数。可以用它来生成直方图：

生成正态分布直方图

会得到类似于这样的输出：

0	*
1	
2	
3	*
4	**
5	*
6	***
7	**********
8	*************
9	*******************
10	***************
11	**********************************
12	*********************************
13	**************************************
14	*********************************************************
15	***************************************************
16	**********************************************
17	******************************************
18	*************************************
19	********************************
20	****************************
21	****************
22	********
23	*******
24	****
25	**
26	
27	
28	
29	

24.8 标准数学函数

标准库提供了常用的标准数学函数（sin、cos、log等），定义在<cmath>中。

标准数学函数均提供了float、double和long double参数类型。

如果数学函数无法计算出数学上合法的结果，它会设置全局变量errno（定义在头文件<cerrno>中）。例如：

errno = 0;
double s2 = sqrt(-1);
if (errno) cerr << "something went wrong with something somewhere\n";
if (errno == EDOM)      // domain error
    cerr << "sqrt() not defined for negative argument\n";

errno = 0;
double p = pow(very_large, 2);     // not a good idea
if (errno == ERANGE)    // range error
    cerr << "pow(" << very_large << ",2) too large for a double\n";

如果需要做严格的数学计算，在计算完成之后应该检查errno，确保它仍然为0。哪些数学函数会设置errno以及会使用哪些值请查阅标准库文档。

注意：标准数学函数遇到错误时会设置errno，但计算成功时并不会将其清零。因此下一次计算前必须通过errno = 0手动清零。

注：标准数学函数支持两种类型的错误处理机制：错误码errno（定义在<cerrno>中）和浮点数异常(floating-point exception)（定义在<cfenv>中）。浮点数异常并不是真正的异常，而是用整数表示的状态标志位。

头文件<cmath>定义了表示标准数学函数使用的错误处理机制的宏常量：

宏常量	值	含义
MATH_ERRNO	1	使用错误码errno
MATH_ERREXCEPT	2	使用浮点数异常

宏常量math_errhandling表示编译器实际支持的错误处理机制，其值为MATH_ERRNO、MATH_ERREXCEPT或MATH_ERRNO | MATH_ERREXCEPT（即二者都支持）。可以通过位运算符&测试：如果math_errhandling & MATH_ERRNO非零，则编译器支持错误码机制，否则errno始终为0。

注意：并非所有编译器都默认开启了errno和浮点数异常，必须通过特定的编译选项来开启或关闭。见简单练习24-4相关的问题Issue #18。

24.9 复数

复数(complex number)及其标准数学函数定义在<complex>中：

template<class T>
class complex {
public:
    constexpr complex(const T& re = T(), const T& im = T());
 
    T real() const;
    T imag() const;
 
    // operators: = += -= *= /=
};

模板参数T表示实部和虚部的类型。

complex<T>的用法与double这样的内置类型完全一样。例如：

Using cmplx = complex<double>;  // sometimes complex<double> gets verbose

void f(cmplx z, vector<cmplx>& vc) {
    cmplx z2 = pow(z, 2);
    cmplx z3 = z2 * 9.3 + vc[3];
    cmplx sum = accumulate(vc.begin(), vc.end(), cmplx());
    // ...
}

注意，complex没有提供<和%。

complex提供了<<和>>运算符，输出格式为(real,imaginary)，输入格式支持real、(real)和(real,imaginary)。

简单练习

• 24-1~24-3
• 24-4
• 24-5, 24-8
• 24-6
• 24-7

习题

• 24-1~24-2
• 24-4
• 24-5
• 24-8
• 24-10
• 24-11
• 24-12