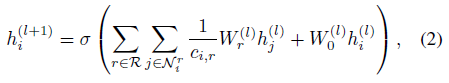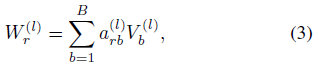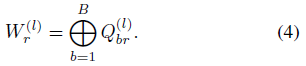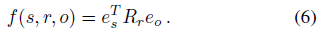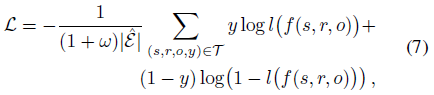【论文笔记】R-GCN
Modeling Relational Data with Graph Convolutional Networks
2018 ESWC
论文链接:https://arxiv.org/pdf/1703.06103
代码:
1.引言
将GCN应用到异构网络的连接预测和实体分类任务
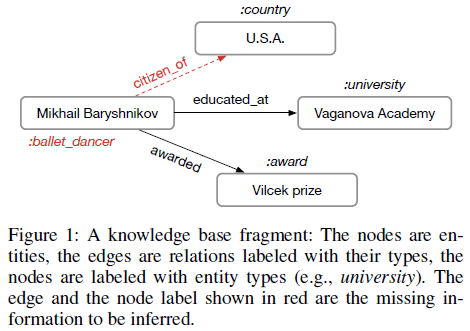
统计关系学习(statistical relational learning, SRL):预测知识库中缺少的信息
该论文考虑两种基本的 SRL任务:
- 连接预测:恢复缺少的三元组
- 实体分类:给实体赋予类别属性
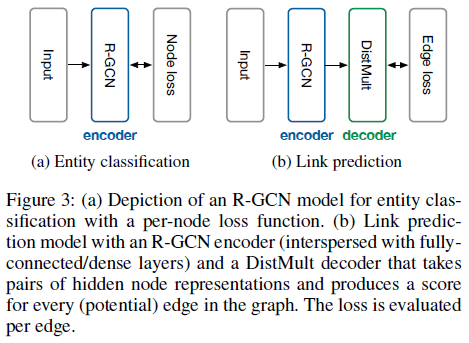
实体分类模型使用R-GCN学习顶点表示,将顶点表示输入分类器预测标签 连接预测模型可以看做一个自编码器,编码器:R-GCN,产生顶点表示;解码器:使用顶点表示和打分函数预测边
2.神经关系建模
定义:多关系图G = (V, E, R),顶点(实体)vi∈V,有标签的边(关系)(vi, r, vj)∈E,r∈R是关系类型
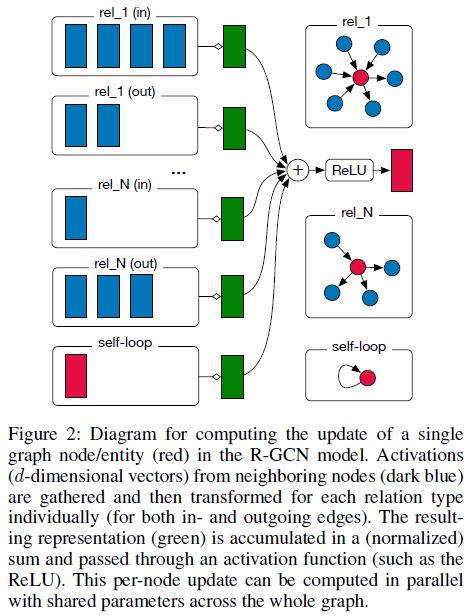
2.1 关系图卷积网络(R-GCN)
多关系图中顶点vi的消息传递模型:
其中 $N_i^r$ 表示顶点vi在关系r下的邻居集合, $c_{i, r}$ 是问题相关的归一化常数(例如 $\vert N_i^r \vert$ )
上式将GCN扩展到多关系图上,每种关系下的邻居分别聚集,最后再求和 这个图编码模型叫做关系图卷积网络(R-GCN),如图2所示
2.2 正则化
(2)式的一个主要问题是参数数量(权重矩阵)会随着关系数量的增加而快速增长,很容易导致出现次数很少的关系上的过拟合以及模型过大等问题
该论文引入了两种不同的正则化方法:基分解(basis-decomposition)和块对角分解(block-diagonal-decomposition)
基分解将 $W_r^{(l)}$ 分解为B个基变换的线性组合:
块对角分解将 $W_r^{(l)}$ 视为块对角矩阵:
整体模型是堆叠了L个(2)式定义的层,第一层的输入是one-hot ID向量(也可以是其他预定义的特征向量,如与定点相关的文档的词袋表示)
3.实体分类
堆叠R-GCN层,对最后一层的输出计算softmax作为类别概率,最小化交叉熵损失
4.连接预测
连接预测用于预测新的三元组,给定的不是完整的边集合,而是一个子集,任务是为可能的边(三元组)(s, r, o)计算得分f(s, r, o),从而确定这些边是否存在
为解决该问题,该论文引入了图自编码器模型,由实体编码器(R-GCN)和打分函数(解码器)组成
该论文的实验中使用DistMult作为打分函数:
其中 $e_s$ 和 $e_o$ 是使用R-GCN学习到的实体嵌入, $R_r$ 是关系r对应的对角矩阵(可学习参数)
使用负采样来训练模型,对每个正样本采样ω个负样本(将s或o替换为其他实体),通过优化交叉熵损失函数使模型给正样本的打分高于负样本:
其中T是正样本和负样本集合,l是sigmoid函数,y=1表示正样本,y=0表示负样本
5.实验评估
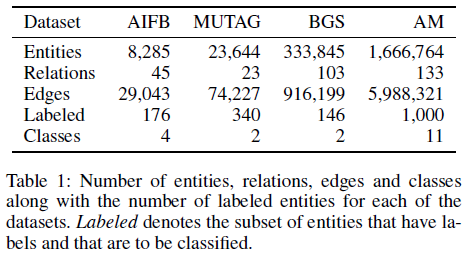
5.1 实体分类实验
实验设置
使用2个R-GCN层,50个epoch,Adam优化器,学习率为0.01,其他参数如表6所示
其中l2 penalty就是优化器的weight decay
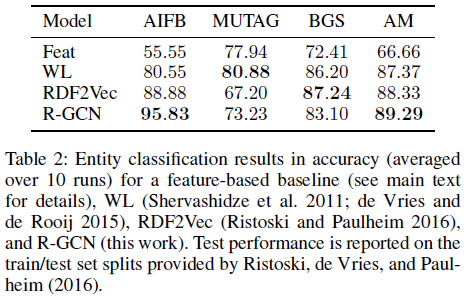
结果
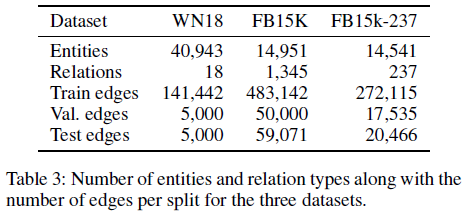
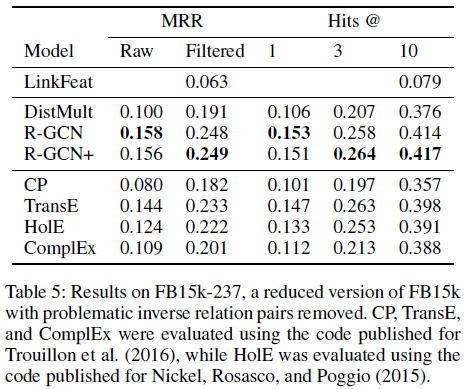
5.2 连接预测实验
数据集
实验设置
评价指标:MRR和Hits@n(n=1, 3, 10),来自TransE论文
\[MRR=\frac{1}{N}\sum_i \frac{1}{ {rank}_i}\] \[Hits@n=\frac{\#({rank}_i \le n)}{N}\]对于WN18和FB15k,使用基分解(B=2),使用1个R-GCN层,嵌入维数为200
对于FB15k-237,使用块对角分解(块大小为5×5),使用2个R-GCN层,嵌入维数为500
自环dropout为0.2,其他边为0.4,l2 penalty为0.01
使用Adam优化器,学习率为0.01
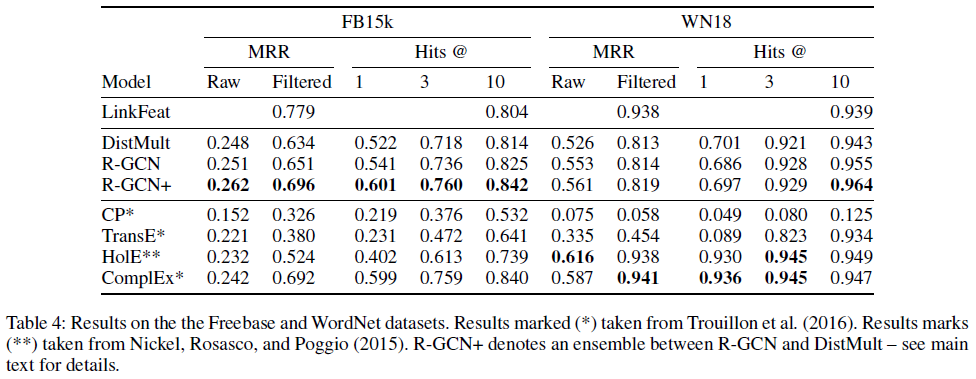
结果